Hello,
Not certain why you are having a problem but I have done this dozens of times with & without column titles.
Just performed another test. From Calc, 27 rows (row 1 headers) and 25 columns to Base creating new table based upon Calc fields. In other words, no predefined table. The went back & selected another 27 rows & 25 columns and appended that to the just created table. No problems.
The first time I used drag & drop. The second, copy & paste. Both work and have ever since I can remember.
EDIT:
Sorry, just re-read your question. It may be you are dropping the data into the wrong place. You drop/paste it onto the actual table name on the main Base screen, not on the view of the table data. Follow the dialog from there. Also you are possibly going to have a problem if copying to a table already defined with keys and those keys are not included with the copy.
SECOND EDIT:
Just want to help in case you are not aware. It appears you are new to Base. Be aware the default embedded DB can corrupt data especially with large amounts of data or even a few embedded images. To avoid this problem, start with a split DB (has upgraded HSQLDB). Instructions found on this post - click here.
THIRD EDIT:
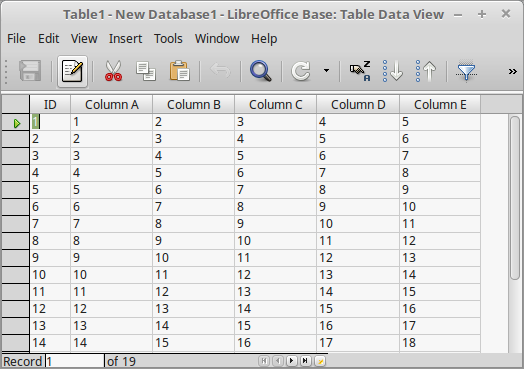
Steps to copy -
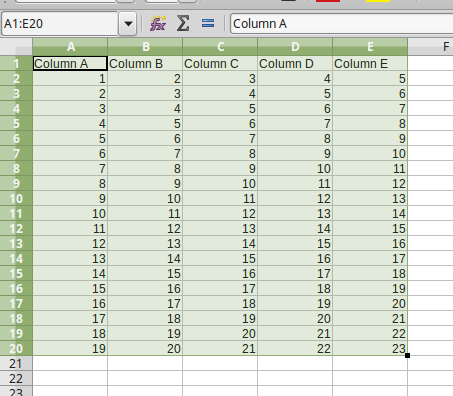
Select data in spreadsheet. In this example the first row will be used for the field names:
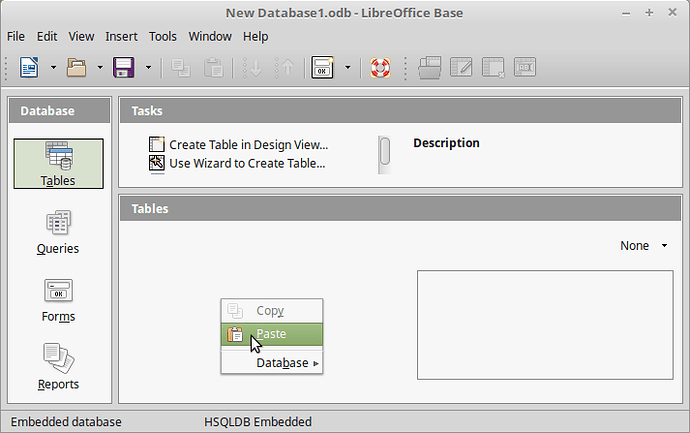
Once selected, right mouse click & select Copy. Next to Base. In Tables (where list of tables occurs) right mouse click & select Paste:
This will bring up the dialog:
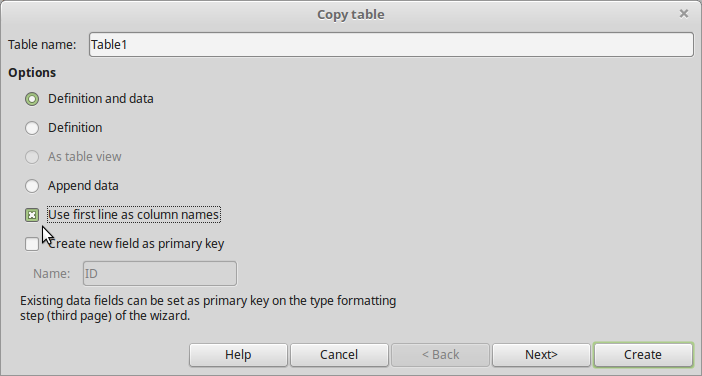
Here table name to be created is at the top (change if wanted), Definition and Data is selected, and because of using Column headers for first row, make sure Use first line as column names is selected.
At this point you can select Create button or Next for further modification to the copying. In this sample, Create was chosen and another dialog appears asking if Key to be added:
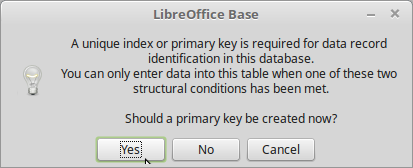
Yes was selected and here is the resulting table: