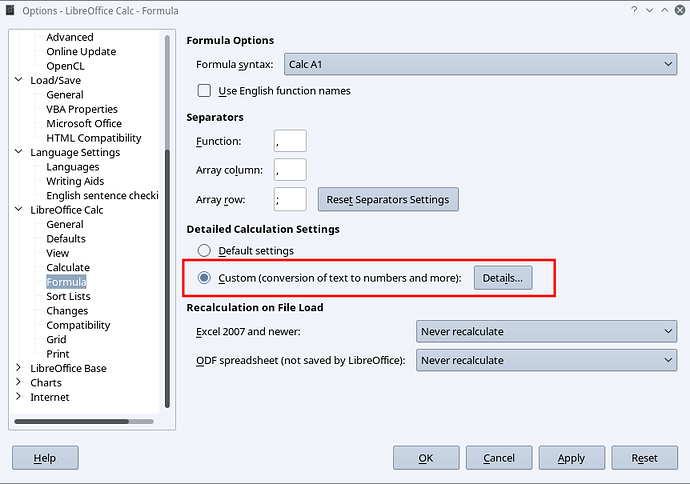
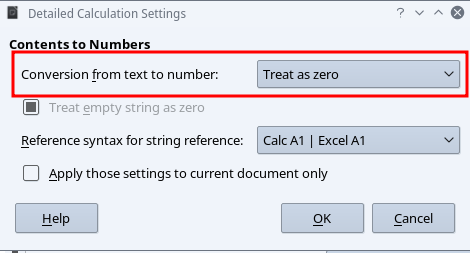
I have a LibreOffice calc spreadsheet, which has the following operation: MMULT(C5:F5, TRANSPOSE(C7:F7)). The operation works as expected, unless the cells are blank or they contain some text. Is it possible to consider blank cells and texts as zeros by default? I want this operation to include cells that haven’t been filled up yet, and might be filled in the future, or could be filled with text. And the operation I described was just an example, I want the rows to extend to its limit. Is there are way to do this.
I’m sorry if this question is trivial, I’m a new to LibreOffice Calc and spreadsheets.