Round to lower on 5

[EL1962]

Hello.

I’ve been looking all the rounding operations, and I didn’t find any to compute values the way I need.

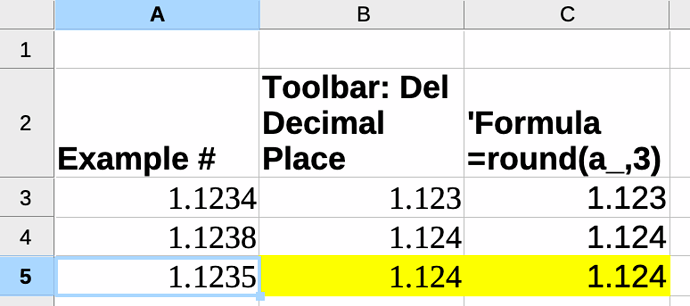
I observed that stock values (mean price, taxes, fees, etc.) are computed using a rather common rule, but with an exception. Examples with 3 decimal digits rounding :

• 1.1234 becomes 1.123 (4 is less than 5, and leads to the lower value)
• 1.1238 becomes 1.124 (8 is more than 5 and leads to the upper value)
• 1.1235 becomes 1.123 <== here is where the rule is broken : 5 is rounded to the lower value.

This occurs each time a value (stock number, stock value) has a 5 factor. According to my banks help desks, it seems to be the rule for rounding operations.

Is there any round function that could apply the same rule ?

Thanks for your help.

Regards.

[Villeroy]

banksters_rounding2.ods (18.6 KB) (updated)

[mikekaganski]

Banker’s rounding is not “half to lower” (as in your file), nor “half to zero” - it’s “half to even”. I.e., 1,235 should round to 1,24, and 1,245 should also round to 1,24.

[mikekaganski]

@EL1962

• 1.1235 becomes 1.123 <== here is where the rule is broken : 5 is rounded to the lower value.

Your example is wrong. In this case, the “usual” rounding to 1.124 is expected; but the difference is at “1.1245 becomes 1.124”. See Banker’s rounding.

[Villeroy]

OK, OK. More like the updated file?

[EL1962]

Hello.
I’ve had a look at you example, and it seems to be an acceptable alternative to a basic macro.
In parallel, I’ve tried using a custom macro that call the Basic round function that seems to follow the “even rounding” that banks use. It’s still not very clear for me…
Thanks for your help.
Regards.

[EL1962]

Hello again Mike.

You’re probably right : my example is wrong. Never thought before rounding was so difficult !

I’ve tried the Basic function and tested a small macro from a sheet. The basic function in fact seems to follow the banker rule. Examples using Round(X, 3) :

|0,1215|0,122|
|0,1225|0,122|
|0,1235|0,124|
|0,1245|0,124|
|0,1255|0,126|
|0,1265|0,126|
|0,1275|0,128|

My macro is :

Function Round_Banker(Optional value, Optional decimals)

 	If NOT IsMissing(value) AND NOT IsArray(value) AND NOT IsMissing(decimals) AND NOT IsArray(decimals) Then
		Round_Banker = Round(value, decimals)
 	Else
		Round_Banker = Null
 	End If

End Function

I’m going to replace the round function in some of my formulas in one sheet and verify that my bank and me get the same rounded values before changing more sheets…

Thanks a lot for help and especially for explanations : I’m sure they can help others too.

Regards.

[EL1962]

Hello again (once more).

Well, after checking some of my sheets, I’ve seen some cases that do not match the rule.
Example : 71 * 0.5% = 0.355 and both Calc and Basic round functions give 0.36, and however my bank’s value was 0.35. This example doesn’t follow neither the even rounding rule, nor the ‘usual’ one. Some time ago, I’ve tried truncating the unused decimal digits, but even if some values seemed to be better, this didn’t solve all the differences between the bank values and mines.

But I guess that this is not anymore a LO issue… I don’t know is someone can explain what bank computers do …

Thanks again.

Regards.

[mikekaganski]

@EL1962

Never thought before rounding was so difficult !

@EL1962

Example : 71 * 0.5% = 0.355 and both Calc and Basic round functions give 0.36, and however my bank’s value was 0.35. This example doesn’t follow neither the even rounding rule, nor the ‘usual’ one.

Heh…

No, this example follows the Banker’s rounding, yet it also shows the binary representation imprecision.

There is no IEEE754 binary 64-bit number (which is used in Calc, and in ~all other spreadsheet software) equal to 0.355; instead, there is

0.354999999999999982236431605997495353221893310546875

which is in binary form:

0 01111111101 0110101110000101000111101011100001010001111010111000

And that number is slightly smaller than 0.355, and thus, rounds down correctly (because rounding happens not from exact half).

Calc possibly gets a bit different value when calculating 0.5%, which is a bit larger than 0.355. Likely, some cancellation takes place…

[sokol92]

This explains, but does not justify, the mistake made by the bank (if the bank does use banking rounding). Bank calculations should not depend on computer standards.

[sokol92]

If we need to use exclusively Calc functions, then we can try this approach:

=IF(ABS(MOD(A1;1/100)-5/1000)<10^(-14); A1+5/1000*SIGN(A1)*(1-2*ISEVEN(A1*100)); ROUND(A1;2))

[EL1962]

Hum… this looks like some bad movie’s end when you think the evil is defeated, but then something shows you it’s not… and let you waiting for the next episode.

So, if I understand, I’ll never be able to get the matching values as long as my bank’s computers and mine, although both use the same rounding algorithm, do not produce the same result because of distinct accuracies, right ?

In some cases, replacing the rounding function with the Basic one may produce more suitable values, but in other cases results will always be different, without being wrong.

I’m not sure to understand why sofisticated IEEE norms do not ensure that two modern softwares (I hope my bank is not still running Cobol programs on the good old IBM 36 I had as a student) compute the same operation with the same result…

In the given case, I’ve saved 0.01 € : that was the good point of the story

Have a nice weekend !

[mikekaganski]

Bankers rounding

tdf#142922 is fixed now in v.7.2, allowing to use Round BASIC function in a user-defined function for proper banker’s rounding.

[EL1962]

Hello Mike !

It seems that your links are all about the same concern I’ve tried to explain, AKA “bankers rounding”, but I don’t really understand how I can get a solution from it to make my “bankers” formulas work.

At least I’m happy to see that my problem is already known…

I’m using LO in version 7.4, and I can’t see any function with some flag to use this rounding mode. Do you mean that a VBA function, since it’s been fixed for MS VBA compatibility, could be a solution ? How can I change my formulas to use such a VBA function ?

Thanks for your help.

Regards.

[HerCorns]

Good day EL1962,

I tried to emulate your rounding issue by using two methods to round to the 3 decimal places, as seen in the picture.

There is a formula you can use "=round(data, decimal places) which should give you the rounding as displayed in the picture.

The rounding of 1.1235 → 1.123, is correct for significant figures, but LO does not use it, it gets only used in scientific measurements.

To show the community your question has been answered, open the More icon. Then click the Solution to the correct answer. To “upvote” by clicking on the ^ arrow on the left of any helpful answers. If you like the post, click on the heart icon.