45.95 - 46.57 = -0.619999999999997 (should be -0.62 exactly; no rounding)

[NOYB]

Open new calc spreadsheet
Enter this formula in cell A1 =45.95-46.57
Cell A1 displays -0.62 as expected.

But formulas that reference cell A1 get -0.619999999999997

45.95-46.57 equals exactly -0.62
There should be no rounding error.

Cut and paste cell A1 to B1 as values only
Cell B1 displays -0.619999999999997

Version: 25.2.5.2 (X86_64) / LibreOffice Community
Build ID: 03d19516eb2e1dd5d4ccd751a0d6f35f35e08022
CPU threads: 8; OS: Windows 11 X86_64 (10.0 build 26100); UI render: Skia/Raster; VCL: win
Locale: en-US (en_US); UI: en-US
Calc: threaded

[Zizi64]

It is a generic “problem” of the different numerical systems.

1/3(dec) equals an endless decimal fraction in the decimal system: 0.333333333…(dec)
1/10 is a simple number (0.1) in the decimal system, but it is an endless binary fraction:
1/10(dec) = 0.1(dec) = 0.00011001100110011…(bin) = 1/16(dec)+1/32(dec)+1/256(dec)+1/512(dec)…

Sometimes the operands or the result cannot be depicted with a simple, short number in a binary based computer.
Use the function Round to rounding the results to the desired decimal places.

[koyotak]

@Zizi64

generic “problem” of the different numerical systems

supplementary:
-0.62 is the analog calculated result, whereas -0.61999… is the digitally calculated result by any microcontroller. Both are correct, which every programmer needs to know. The binary phenomenon occurs when switching from the positive quadrant to the negative one, because the negative sign doesn’t exist in binary and is instead preceded by a “1” as a pseudo MSB (most significant bit). This pseudo MSB is not a numeric value like all subsequent binary digits “0” and “1.” Theoretically, one could add the “difference value” to the analog result if one knew how small it would be: 1^(-12)…1^(-1024).

In the digital system, only addition is possible by comparing the two bits and carry over to the more significant bit. Subtraction is performed as the addition of a negative number. Be aware that the analog world, the digital-electrical world, and the binary-programmatic world lead to translation errors.

[koyotak]

@Zizi64

1/3(dec)

Mathematically, =1/3 is the final solution to an analog calculation, while 0.333… only returns an approximate number: ≈0.333, which also only represents =0.(overlined)3.

I remember a technical article that suggested a different approach: instead of dividing n by 5, which leads to just such an “error” because no microcontroller can divide analogically, one should divide the formula by n × 2 / 10, the doubling is performed as an addition to itself, and this result is shifted bitwise by one bit position to the “right.” I was astonished by this; I must have been asleep at the technical college!

[ajlittoz]

And this “trick” does not change anything (apart perhaps speed) because 1/10 = 1/2 × 1/5 and 1/5 cannot be represented exactly in base 1/2 because 2 and 5 (which are primes) are relatively primes to each other (I should write 1/2 and 1/5 but the result is the same). Fractional bases lead to this phenomenon unless you convert into bases which are integer multiples of each other.

EDIT:
The main problem in the kind of question like this one is a lack of education. Computers are now present everywhere and fundamentals are no longer taught. Thus lay users take for granted (considering the incredible achievements made possible) that computers always provide exact arithmetic results. Unfortunately, they are quite dumb, only being able to deal with signed integers. All other types of numbers (fractions in Q, reals in R, complex in C) are simulated as approximate integer values. Note that base 1/2 (and similar) is an “artefact” caused by moving the “decimal point” from right to extreme left. This shift brings also its share of problems.

When computers began to be ubiquitous in the '70s and '80s, every “technical” training program had a module about numerical analysis applied to computer calculations. Nowadays, this kind of module is deemed unnecessary and graduates have no idea about the tons of issues resulting from bad computation methods. And I don’t speak of non-technical average Joe.

The most terrifying time bomb is that even computer students are not made aware of the mathematical issue because emphasis is now put on GUI, internet or object theory. After graduation, they may be hired to create technical or business suites without consideration for the intrinsic traps.

Please, forgive my rant (it is probably off-topic).

[karolus]

btw.
If we calculate the circumference of a circle with a diameter of 10,000.00 km, we obtain an error of ~ 63 nanometers when rounding PI to 15 decimal places, compared to a much more accurate value for PI.
This corresponds to approximately the distance between 200 water molecules placed side by side.

from decimal import Decimal
from math import pi
false_pi = Decimal('3.141592653589800')
mostly_true_pi = Decimal(pi)
print(f"⇒⇒ {mostly_true_pi}")
print(f"⇒⇒ Error = {((false_pi*10000)-(mostly_true_pi*10000)) * 10**12 } nano_meters") # m # mm # µm # nm  
####
⇒⇒ 3.141592653589793115997963468544185161590576171875
⇒⇒ Error = 68.84002036531000000000000 nano_meters

[CRDF]

Of course I know some arithmetics, but here this doesn’t happen…
(?)
24.2.7.2 (X86_64) / LibreOffice Community
Build ID: 420(Build:2)
Ubuntu package version: 4:24.2.7-0ubuntu0.24.04.4

[ajlittoz]

Are you sure? Which is the cell format? What happens if you set it to 0.0000000000E+00? Reminder: this does not change the value, just how it is displayed.

[CRDF]

Cut & Paste to C1
D2 = C1 + D1 (1)
D3 = C1 * E2

[newbie-02]

@koyotak

is the digitally calculated result by any microcontroller

from this point on we disagree. A.) there are native decimal CPUs, IBM, B.) what binary CPUs calculate depends on the numerical system / datatype you use, C.) there are qualified decimal systems available.

[karolus]

@newbie-02

C.) there are qualified decimal systems available.

yes…available in theorie, but in practise they are 5 to 10 times slower than good old double-precision-foating-point algorithms!

[ajlittoz]

@newbie-02

C.) there are qualified decimal systems available.

And they won’t solve all cases: if your arithmetic value is not a strict decimal one, you’re back to the problem. Unfortunately there is no perfect solution to this arithmetic problem. It is a matter of primality and you can avoid it.

[newbie-02]

@karolus

but in practise they are 5 to 10 times slower than good old double-precision-foating-point algorithms!

maybe, however that doesn’t harm a spreadsheet in any way, the bottleneck are users and display. No user realises if a recalculation lasts 0.2 microseconds or 1.0, and in output - on screen - decimal formats beat binary up to 1:10, in a very costly operation. Add two values in bin64: 6.9 CPU ticks, dec64: 92, read in 0.9999999999999999 in bin64: 283 ticks, in dec64: 105 ticks, print out 0.9999999999999999 from bin64: 788 ticks, from dec64: 36 ticks.
What does Calc do when a user changes a cell? Recalculate the chains dependent on that cell, and printout some ~300 cells on screen. Evtl. prepare some 8, 24 or 48 times more around the display frame for faster scrolling.
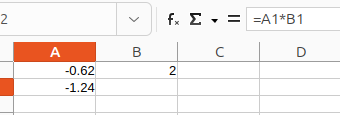
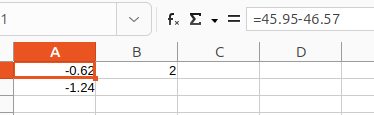
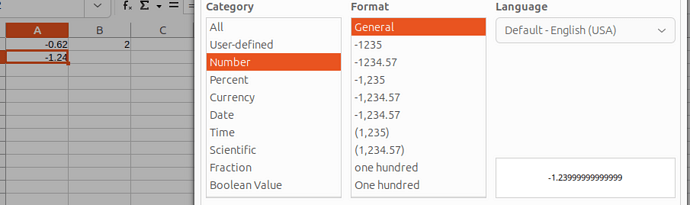
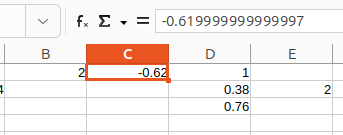
Estimate which datatype serves better.
Just ask users what they would prefer? Having some number crunching calculations a little slow ( let’s say I tested a testsuite without! output to 600 instead of 350 seconds ), with decimal correct results, or quick with most results “a little off”, and some completely nonsensical.

@ajlittoz

And they won’t solve all cases:

Yes, admit, however A.) do come near to what users are used to, enable man - machine harmony, !PREDICTABILITY! what the results will be. And B.) nobody forbids hybrid models which - with some more effort - serve a mode by users choice.
The evil is pretending “decimal” while not sufficient, the second evil is not to tell the users in advance, the third evil is to ignore decimal datatypes because “slow” ignoring their capabilities and options to improve, the fourth evil is to wrongly tell users - or me - decimal would be impossible.

[koyotak]

@ajlittoz

arithmetic value

Let me throw in a real-life analogy: You have several ways to get from one floor to another. If you can fly like a butterfly, you’re an alien. Your feasibility is therefore limited. Using stairs and a ladder, you move digitally step-by-step; using a rope and a slide, you move analogically. With the latter two, you can assume any intermediate position, something you’ll never achieve with the first two, no matter how many smaller intermediate steps are integrated. There will always remain those “non-tolerated” areas in between that can’t be clearly assigned — not even with hysteresis feedback. Fuzzy topology was invented as a helpful solution in the multi-stage digital realm…

All those problems and therefor much more are inherent in every topology of hardware A/D- and D/A-converters. We can decide whether their inaccuracies are tolerable or not. If the salesman dictates a cheaper model, then we engineers have to do hypocritical gymnastics to avoid accepting such large deviations, often with some kind of fatal consequences at some point.

[ajlittoz]

@koyotak: this will be my last comment

When using a tool, you must follow its usage rules. For instance when driving a car, law tells on which side of the road you must stay. If you viloate the rule, you’re in danger.

In your case, the difference between 0.62 and 0.619…77 is 3 10^-15, i.e. in relative value 5 10^-13. Such a tiny difference is negligible in most practical situation.

I agree with you that a human prefers to read 0.62. This is the role of cell format where you specify how many digits you want to see and Calc will do the visual rounding.

This is for general-purpose calculation. You are in an accounting context. This context also introduces rounding conventions (not truncation). This rounding is necessary every time you multiply or divide to reconcile what you (want to) see and the value kept in the record.

To do that, I systematically write =ROUND(…; 2) around accounting formulas involving multiplication and division. By doing so, I make sure that the value shown is exactly the same as would be used in later calculations. To avoid “cent errors” (as can happen if you SUM() “raw” values and in parallel rounded values, you must follow a strict discipline where you chain only rounded intermediate values, not recomputing them every time you need them (this means your formulas in the end are extremely simple because you store in separate cells scratch intermediate values when they have an accounting sense).

The discrepancy between displayed and “mental” value occurs whenever you have a fractional base in your floating-point number representation. Even if you have a decimal floating-point unit (base 1/10), the fact that the distance between two successive stops in the numbering set is proportional to the number order of magnitude. Thus the scale is quantized with a variable step. You can’t avoid this if you want floating-point, i.e. a huge range.

Old business computers had decimal arithmetic. But this arithmetic was integer-based, not fractional. Since this was used for accounting, floating-point was not necessary. You only had to keep track of where the decimal point would end up after an operation. It is not complicated but requires programming. This was entirely handled behind the scene by COBOL or PL/1. Spreadsheet are not programming languages and try to provide an easy interface to simple tasks. However, every user has his/her own original purpose. This can’t be accounted for universally. This is why TRUNC(), ROUND() and other functions are provided to fulfil th specific needs.

If you want some insight about the issues with fixed decimal and floating-point arithmetic, I encourage you to read Donald Knuth’s Art of Computer Programming, Vol. 2, Semi-numerical Algorithms.

I remember having read an algorithm for outputting a floating point number and avoid printing senseless digits like the final …99997 above. It tried to decide whether the last bits of a number where meaningful or not. This seems very appealing but I lost the reference. It could have been from some IEEE Proceedings or an ACM publication.

[koyotak]

@ajlittoz

Please, forgive my rant (it is probably off-topic).

It is on-topically! To better understand and comprehend the brutal, real and very complex world. Without wanting to discover the mythical formula of how our world is composed.

Yours tiny peephole offers a brief impulse to plunge deeper into the intimate stratosphere, which a technician must often painfully endure the more experienced they become, fleeing the swamps of all theories within the atmosphere.
Just to gain that microscopic knowledge of how large the iceberg beneath the water’s surface can even be, which the theoretical teacher fails to even hint at. Training courses and universities are far too intellectual. How often have I had realized that their theories were, at the workbench, figments of my imagination. Example: Why do I need the 6th decimal place of pi when the circle drawn with chalk on the blackboard already has an unstructured width of several millimeters thanks to the rough surface of the blackboard? And what does the jigsaw do to the wooden board, no matter how precisely I try to guide it? Or: How can I dictate to the PCB manufacturer via e-CAD that such-and-such a trace must have a width of 7 μm, without knowing how much the chosen PCB manufacturer will underetch or overetch, thus transforming the ideal rectangular cross-section into a rounded or square surface? Only to discover during electrical testing that the distance to the adjacent copper trace has critical points. As a technical illustrator, I experienced countless ups and downs and was impressed by the heights from which academics looked down on me, or up to me, a non-academic. I was also impressed by how important the displayed millivolts of the mains voltage of a multimeter display were to electricians! Which inspired me to research the tolerance ranges of all.

[karolus]

@koyotak
You didn’t escape from the play »The Physicists,« did you?

[NOYB]

Even the cheapest of calculators is able to give correct results of addition and subtraction.
Even the builtin Microsoft Windows calculators can give the correct results.
Even old clunky desktop adding machines of bygone eras give the correct results.

Yet here we are in 2025 and spreadsheet developers/engineers/programmers can’t give correct answer of 1st grade subtraction.

Applying the ROUND function to every subtraction to get correct answer is pathetic. Computers can do that to accommodate humans rather than humans accommodating computers.

Everybody knows the precision of addition/subtraction is equal to that of the most precise operand. Program it. i.e. accommodate humans.

[mariosv]

It’s funny, Microsoft engineers can do it with the calculator, but not with Excel.

[Zizi64]

Maybe the Microsoft engineers use some rounding in the Calculator BY DEFAULT, but not in the Excel.
YOU must use rounding functions in the Excel - if you need them.