[edit]
increasing the urgency, i have reproduced the issue here cleanly within the ‘15 - 16 decimal digit accuracy range’ claimed by calc, as well as with old versions back to 3.5.1.2, as well on another system (linux with an older LO 7.1 alpha),
this eliminates almost all local influences, unless Intel Xeon or Lenovo have a very exotic bug,
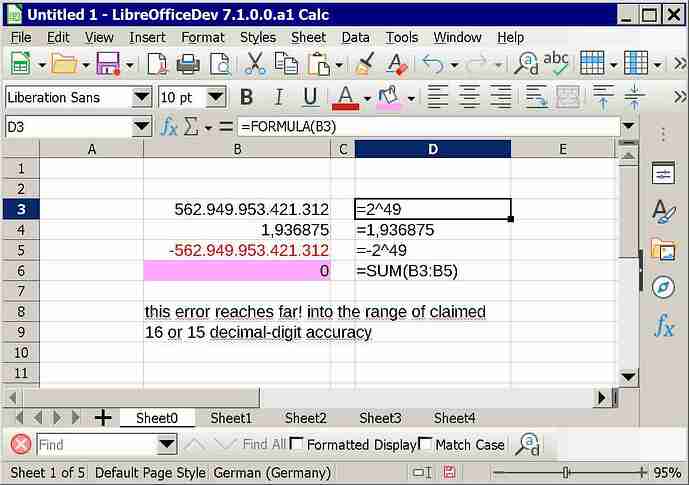
since calc calculates more precisely for the status line - which calculates / rounds differently according to @erAck - i think ‘error in LO’,
and! the error is not ‘only rounded for display’, it is! affecting downstream calculations,
i’m actually quite sure about the bug, on the other hand it’s hard to believe that such an inaccuracy could survive undiscovered in calc for such a long time … to be sure that it is not some exotic fail here, or e.g. a special option that other users don’t set like i do, it needs external tests, please type in the example from the short screenshot and comment if you calculate ‘0’ or a somehow reasonable value,
thank you very much, you can save me hours of experimenting with that …
[/edit]
Miscalculations in calc? Request for a cross-check
i have had the impression for some time that calc sometimes miscalculates, when i complained about it it was mostly explained with ‘fp-calculations’, ‘rounding’, ‘calculations better than rounded display’ and the like …
- the problems are ‘not so easy’ to catch and nail down because often hidden behind rounded display -
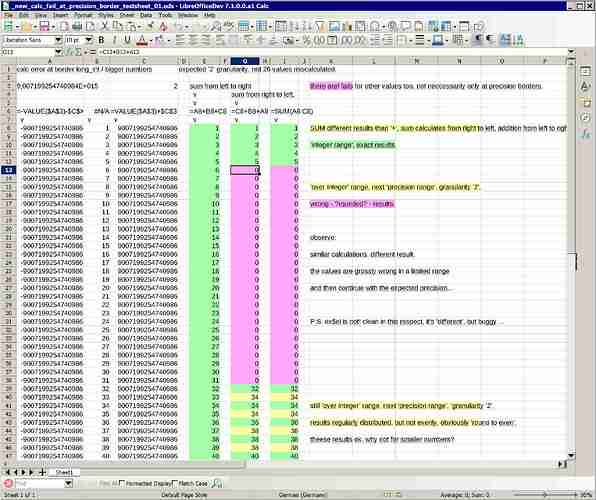
today i could narrow down two such strange things and think that they are rather bugs than ‘fp-shortcomings’, before i annoy developers unnecessarily i ask for a countercheck … error? or ‘the child is not squinting, it should look like this’? or are the values calculated better on other systems?
see sample file for own experimenting, - click to download - and
…