Can Calc return which combinations from a list approximate a particular sum? If so, how?

English
, ,
#1

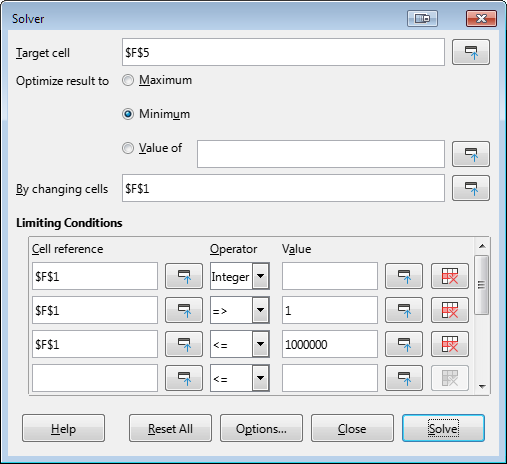
[edited] In column D of a sheet are the respective total areas of each of the 50 US states, plus DC, PR, USVI, and a couple of others (cells D3:D59). I got the numbers that I’m using from Wikipedia, so the numbers may not match official sources; for now, this is close enough. I want to know which combination of areas most closely approximates an arbitrary value.

I haven’t been through every possible combination, but the combined total areas of Alaska, North Carolina, Delaware, Rhode Island, Guam and the US Minor Outlying Islands exceeds by 0.48 sq mi my first arbitrarily-selected target of 722.832.95 sq mi (the area of a 960-mile-diameter circle). There may be other combinations that are closer or even exact, but finding them manually promises to be an exercise in frustration.

ps: Apologies if the correction bothers anyone: I added a column (A) indicating the original relative line numbers, so that no matter how I sort the data in columns B through M, I can easily restore the original sort even if I forget what it was. Additional info is in my comment to the first answer.

#2

Basically this looks like a rather ticklish problem of mathematics.
A brute-force solution would require to generate all the subsets of your 57 single areas, the so-called power-set, which has - the empty set excluded- 2^57-1 (about 144 115 000 000 000 000) elements. Since a spreadsheet “only” has 2^20 (1048576) rows this isn’t a task for Calc.

#3

@Lupp And if you go for a trick? Since a very accurate result is not needed, only as close as possible, the number of options can be greatly reduced and a solution can be found in Calc in a reasonable time.

#4

@JohnSUN: What’s the kind of trick you have in mind?

Of course, I also wouldn’t actually check 2^57 subsets, but concerning a selection of good (and then better) approximations spreadsheets also aren’t what I would suppose to be a good tool.
After all the questioner seems to look for a very good approximation since he already combined the largest (Alaska) and some of the smallest areas. Why shouldn’t be there a better approximation replacing Alaska with a dozen-odd areas of a medium size?

(Editing: Meanwhile I looked at your answer, but I didn’t understand it yet well enough.)

#5

@Lupp In the 2011year, I already wrote a macro that does something similar - selects the set of invoices to pay for the specified amount. There’s a simple recursive function. But in order to present that macro as a solution to this problem, I must re-read the code and, perhaps, adapt it a little. Therefore, for now, I suggest using Solver.

#6

@Lupp.
AFAIK, to perform the evaluation in a spreadsheet, the data set needs to be present for reference, and the selection matrix is internal to the sheet, so the first 2 columns in the reference sheet can contain 57 x 18,396 = 1,048,572 data cells (so I lose 4 rows per tab, but the relatability of the info is hugely improved versus a completely-populated sheet).

This gives 18,396 x 511 = 9,400,356 combinations that can be tried in the first tab, and 9,418,752 combinations that can be tried in each successive tab. I would therefore need only a total of 872,150,123,533 tabs; obviously, this would require multiple sheets and something more along the lines of a fairly modern Cray just to load and process.

A better approach would likely be a database, but I haven’t programmed one of those since Lotus 1-2-3 was considered bleeding-edge tech, and “my skills is nils” these days.

#7

Look guys, I’m not very good at combinatorics, I don’t understand at all what matrices you are talking about, and I am absolutely unable to read these giant numbers that you show to each other. Perhaps you know something about these fifty … well, fifty-seven states that I don’t. But let’s approach the problem from the everyday point of view. If you, buying a can of Cola, gave the seller $ 100, and he began to calculate all the options for counting change, then you would stand in front of him forever. However, somehow the purchase is done quickly enough, right?

#8

@HavaneissDei: I don’t think that the full generation of all the subsets is a reasonable approach at all, and I also can’t see advantages of a database in this case.
The problem is clearly to find a good algorithm, imo.
A recursive “fill-up-next-to–and-try-better-then” (what also JohnSUN may have in mind) should be appropriate. (If the absolute difference shall be minimized, an extension of the approach is needed.)

@JohnSun: I only mentioned the big size of the “power-set” to disqualify the “check-them-all” approach.
The change problem, seen the pragmatical way, is much simpler, imo. (It gets a bit more demanding if you can ask the customer to reconsider the pieces he gave.) Anyway: The master of the mint created pieces making the thing simple. The master of the countries didn’t.

#9

@JohnSUN: We were describing the “limitations” of the spreadsheet size: Columns A through AMJ =1024 (=2^10); the count of rows potentially available in any particular tab is 1,048,576 (=2^20); the matrices represented how that could (mathematically, not practically) be done, if I were to do a brute force exercise in which every possible combination was attempted, regardless whether it was reasonable towards satisfying the objective. Lupp and I were agreeing that route was both absurdly impractical and impracticable; I just went the extra step in showing how huge that sort of approach would be.

I think the algorithm approach makes sense, but … I started with a hypothetical circle of 960 mi diameter; half the diameter and you get 1/4 the area: now Texas and Alaska can be excluded because they’re much bigger than the target. “IF” can perform that sort of exclusion, but it still leaves the change-making mess (cf: Lupp’s take on your analogy) to be solved.

#10

@HavaneissDei Thank you for an interesting task, I was seriously carried away by it. I also took the area data for each State from Wikipedia. I did some experiments - there are really a lot of combinations, but not at all as many as you and @Lupp calculated.

The shortest sequence (not the only one!), apparently, “163695(CA)+104094(CO)+10932(HI)+82278(KS)+40408(KY)+53819(NC)+268596(TX)=723822”. And the longest is “52420(AL)+5543(CT)+2489(DE)+65758(FL)+59425(GA)+10932(HI)+57914(IL)+40408(KY)+52378(LA)+35380(ME)+12406(MD)+10554(MA)+48432(MS)+9349(NH)+8723(NJ)+54555(NY)+44826(OH)+1545(RI)+32020(SC)+42144(TN)+9616(VT)+42775(VA)+24230(WV)=723822”. By the way, you threw out Texas in vain - you can see that it entered the short set.

#11

What I gave as the number of possible combinations wasn’t reduced by any considerations concerning the target or number of used (allowed) addends, or …
It was the number of combinations you get if you decide for every single addend whether it should add in or not. For 57 addends this number is exactly 2^57.
Of course there are lots of ways to exclude combinations in advance of actually testing them.
See also my answer.

#12

Try this option - perhaps this solution will satisfy you.

Add such cells not far the list of states

Calc Cells.png
Calc Cells.png709×141 4.59 KB

And next to the list of states, add a column with the formula

=BITOR($F$1;(ROW()-1))=$F$1

Perhaps your formula should be different. My test list of states starts at cell A2, so I could use (ROW()-1) to renumber them from one.

You can set the format for this column like "*";"";""; - then instead of the set TRUE / FALSE you will see only asterisks opposite the currently selected states.

Now enter different values in F1 and make sure that for each of them a different set of states is selected and the sums in F3 and F5 change.

Now let’s reformulate your problem - “choose such a number in F1 so that the difference between the desired value and the found sum of areas is minimal.”

Calc can easily solve this problem with Tools - Solver

Solver.png

(I must admit that I don’t know Tools - Solver well, I practically don’t use it. Perhaps someone will tell you about additional parameters that will allow you to solve your problem more accurately)

Sample Approximate a particular sum.ods

#13

I think I may be already doing something like this and calling it “manual.” In O1, I have placed my arbitrary target value; in O2, I have the following formula:
=$O$1-SUM(O3:O59)

In O3, I have the following formula:
=IF(N3=1,$D3,0)

O4 through O59 are filled with formulae patterned similarly to the formula in O3.

By entering “1” in the N-column cell corresponding to the row in which the state’s data appears, the area is put into the stack of values that are summed for comparison and contrast.

It’s very crude, but it is vastly quicker than trying every possible sum. It’s ironic, really: I excelled in algebra and geometry when I was 4 years old; in the first grade, I tutored my teacher’s 12th-grade son in calculus (which then seemed intuitive to me). Today, I do well to perform basic operations (add, subt, mult, div) and the Pythag theorem: with advancing age, I have (imho) literally become mathematically dull.

#14

@HavaneissDei In other words, did you manually select a set of units in column N? Well, I propose to do the same, but fill the entire column based on the value in one cell - let Calc figure out if that row is currently selected by itself. That is, you only need to change one cell. And Solver will automatically change it until it finds an acceptable result.

#15

@HavaneissDei If you are still looking for an acceptable solution, perhaps Setter will help.

#16

I also (like @JohnSUN) was caught by the task, and I meanwhile spent a-few-or-more hours for related considerations.
Thanks to @JohnSUN for his suggestion to use the (a) non-linear solver. I experimented with the idea, and was surprised that there were “acceptable” solutions found within acceptable time.

However, any such proceeding looking for a minimum (the remaining area in our case) suffers from chances to get caught in a “valley” and to spend a lot of time to find the local minimum, while the jump to a deeper valley is blocked (e.g. by a need to change too many parameters at once to find it).

The problems of the kind we face here discussed in theory are known to be “extremely time and storage consuming”. In German the respective term is “NP-schwer”.
What’s acceptble?
If an exact solution is possible (not proven impossible), any approximation has a smell.
There are many interesting variations of the problem.

Anyway I finally decided to create a deterministic algorithm, safely finding the (a) best possible solution with a given limitation to the number of addends. Such an algorithm will need to work with recursions, and I decided to write it in recursive manner. See attachment.

Note: I did not try to optimize efficiency beyond a few steps. It’s really challenging because any approch to better efficiency will require data analysis, and data analysis will require code, storage, and time …

OptimalPartitionEx.ods
The addends must be assured to be sorted descending!

#17

Concerning the term “best solution”:
The algorithm contained in the example attached to my answer can not distinguish between “equally good” approximations based on an additional attribute like “less addends” or the like. To allow for such a distinction would (imo) require to omit the shortcut based on “reminder=0”.
The example of 1234567 km^2 can demonstrate this shortcoming: There is an exact solution with 5 addends, but it won’t be found if you allow for 6 or more addends, because then also exist exact solutions with more than 5 addends, which are tested earllier during the recursions, and by that get finally accepted.
An exact solution with 9 addends is even found rather fast.

Impressum (Legal Info) | Datenschutzerklärung (Privacy Policy)   Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.