I would really appreciate it if someone could evaluate the formulas I have inserted in cells G23 & G30 of the attached spreadsheet based on the mathematical equations to their right and the values in column B & C as they are returning unexpected values. If they are incorrect perhaps someone could offer a solution. Thank you in anticipation.
Buckling Check Spreadsheet.xls (29.5 KB)
And which values are you expecting?
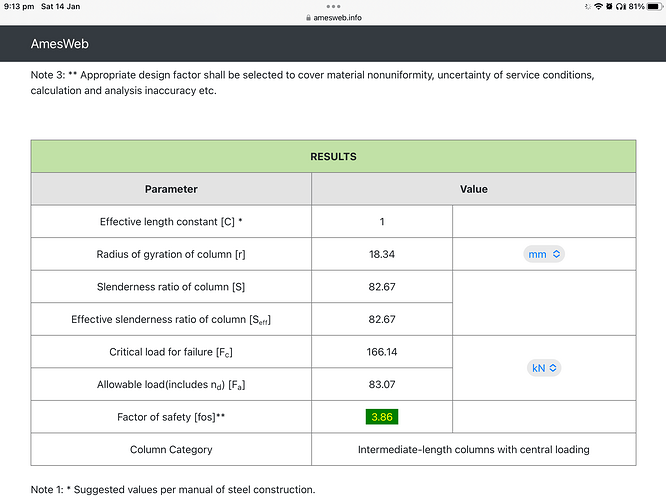
I was expecting the Johnson formula to produce approximately the same as the Amesweb online calculator of 166k or maybe even
up to 182kn. There is a link to the calculator above the formulas ctrl click “source ——-“
See image attached
Which values have you entered to that calculator? Your spreadsheet lacks most units, but the calculator indeed takes them into account. The plain link to the “source” also has no value without those. And that shows why people using math/physics formulas must understand what they do.
Thank you for your help. I took the values from pages 3-16 and 3-14 of these design tables:
[https://www.austubemills.com.au/wp-content/uploads/sites/9/2022/02/atm_dct_sshs_aug13_new-1.pdf]
I was remiss in not including this information.
I will now study your follow up response below before posting again tomorrow.
Your help is greatly appreciated
The formula in G30 is:
=(B32-((B32*B24)/((2*B22*B28)^2)*((B25^2)/B23))*B27)
To make it easier to understand, let’s replace references with respective symbols:
=(Sy-((Sy*L)/((2*Pi*k)^2)*((C^2)/E))*A)
If you analyze it carefully, it is a negation of Sy and ((Sy*L)/((2*Pi*k)^2)*((C^2)/E))*A.
This already shows one error, compared to the original formula:
Pcr=(Sy-(Sy*L/(2+Pi*k))^2*C^2/E)*A
which is a multiplication of Sy-(Sy*L/(2+Pi*k))^2*C^2/E and A.
There is another error, which is only squaring the divisor of Sy*L/(2+Pi*k).
But if you do these corrections, and get the “correct”
=(B32-(B32*B24/(2*PI()*B28))^2*B25^2/B23)*B27
it would give you unexpected -72270279. Why?
Because you must never ignore units of the physical quantities you are dealing with.
Assuming the following source data:
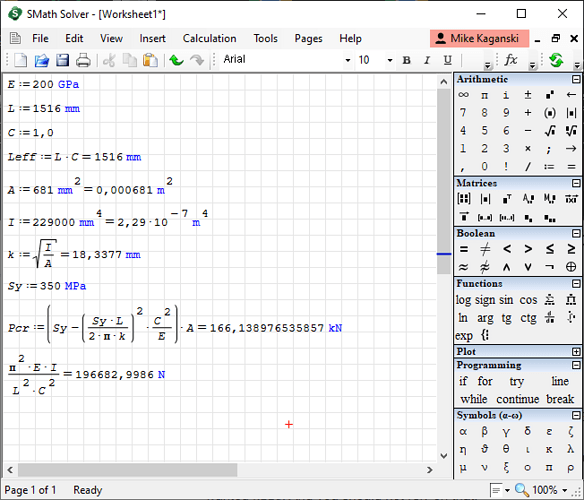
E = 200 GPa
L = 1516 mm
C = 1
A = 681 mm^2
I = 229000 mm^4
Sy = 350 MPa
the correct calculation is:
k = SQRT(I/A) = SQRT(229000 mm^4/(681 mm^2)) = 18.3377 mm
Pcr = (Sy-(Sy*L/(2+Pi*k))^2*C^2/E)*A
= (350 MPa - (350 MPa*1516 mm/(2*Pi*18.3377 mm))^2*1^2/(200 GPa))*681 mm^2
= (350000000 Pa - (350000000 Pa*1,516 m/(2*Pi*0.0183377 m))^2*1^2/(200000000000 Pa))*0,000681 m^2
and the corresponding spreadsheet formula would be
=(B32*10^6-(B32*10^6*B24/1000/(2*PI()*B28/1000))^2*B25^2/(B23*10^9))*B27/1000000
resulting in the correct 166138,976535858 (N), which is the same as the expected 166,14 kN shown on your screenshot. (I had replaced the manually entered value of k in B28 with =SQRT(B31/B27).)
First let me thank you for not only supplying the formula but also the explanation of where I was going wrong. You have gone to a lot of effort and this has really helped me.
Secondly I would like to reassure you that I am not an aspiring young engineer just an old character trying to keep his brain ticking over.
In retirement I have taken an interest in 3D cad modelling and FEM and structural systems. This led me to take an interest in the engineering principles involved.
If you can find the time I have two more questions:
In your formula you have a set of closed bracket () behind the letters Pi - is this the way the Pi function is used by more advanced spreadsheet users?
It looks like I have the formula in cell 23 (euler formula) but despite your explanation I don’t understand why haven’t had to use the ^9 exponent for value "E"in this case. would you mind explaining this to me please.
Buckling Check Spreadsheet_Rev1.xls (69 KB)
Best way to create a formula by usage of the the SI base units. (Pa for the pressure). Otherwiswe the publisher of a formula can enforce to use prefixed units or even non-SI units. You must know (by studying the descriptions) what physical quantities, which numeric values/format and what units (w/wo prefixes) are used by the actual formula.
.
Always do a unit analysis when you use a complex formula with the actual input quantities.
.
Maybe you need the exponent and maybe not. I never used these formulas.
PI is a spreadsheet function; and as such, its call needs the parentheses. Otherwise, it would be considered a name of something (a column name), with a syntax error. And indeed, you don’t need to use any cell for manually entered PI approximation (like C7, C22).
Firstly, I assume that by cell 23, you mean G23.
Then, let me point that your “units of Moment of Inertia (Smallest) being number” is wrong, and it is measured in mm4.
With that in mind, the physical formula there is
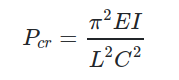
Using the values from my answer above, the correct calculation would be
π^2 * 200*10^9 Pa * 229000*10^-12 m^4 / (1516*10^-3 m * 1)^2
and that gives 196683 N, or 196.683 kN. It just happens that the SI multipliers cancel each other happily in your chosen case to result in final 10^3 multiplier, that matches wanted kilo. And you should not rely on that.
I’d suggest to use programs like MathCAD, or SMath Solver, that allow to use units, and perform required transformation for you.
@ Zizi64 - Thank you for your reply and advice
Thank you once again I will alter the spreadsheet accordingly. I have SMath and have been meaning experiment with it.