A1: 8192,3
B1: 7774,3
C1: =A1-B1
cell format: Standard;-Standard;;
C1:
417,999999999999
?

A1: 8192,3
B1: 7774,3
C1: =A1-B1
cell format: Standard;-Standard;;
C1:
417,999999999999
?
Hello @ANG,
Not with me (see ANG.ods (7.9 KB)).
In your document, A1 and B1 contains formulas, or just numbers? Please, edit your question to add more info. Thanks.
Edit:
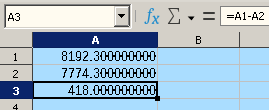
Edit 2:
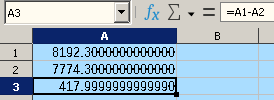
see
bug absent if:
cell format: Standard
also, in FAQ:
“Calculations with those numbers necessarily results in rounding errors, and those accumulate with every calculation”
where here “roundind”? (subtraction)
ps: in MS Excel bug is absent.
If you mean that with “default” cell width, and with plain Standard cell format, you see expected 418, but when you change the cell format to Standard;-Standard;;, it becomes ### in the cell, and when you widen it, you see that imprecise result:
The plain Standard format (unlike any other format, including user-defined formats that use Standard in its parts) has a special property of automatically adjusting to the cell width (i.e., its decimal count adjusts itself to fit into the cell). For wider cells, it shows more decimals; for narrower cells, it rounds to the given width.
So test this: put the same =A1-A2 formula into two cells A3 and A4; have A3 formatted as Standard, and A4 formatted as Standard;-Standard;;; see that A3 shows 418, while A4 shows ### indicating “too narrow cell for the given number”; widen the column to make A4 show its value, and see that A3 (formatted as Standard!) also shows now that “unexpected” result.
Also see that your “in MS Excel bug is absent” only shows that MS Excel, by default, shows fewer decimals, and - as shown by @EarnestAl - shows exactly the same result (which is the result of computer floating-point operations described in the FAQ) when showing enough decimals (12+).
The rounding happens at every operation that converts the decimal number (say, 8192,3, 7774,3) into the binary floating-point number format used internally, and also at every operation where another number appears that can’t fit into this representation. You should not imagine that when you enter 8192,3, Calc keeps 8192,3 inside. No, it keeps 8192,29999999999927240423858165740966796875 (represented as 0 10000001100 0000000000000010011001100110011001100110011001100110 in the IEEE 754 binary64 format), which is not the same number. This number is the closest to what you entered, that can be stored in the machine representation. So rounding (to binary, not decimal rounding!) happened already in A1 (and A2).
thanks… sad, it turns out the calculations are extremely inaccurate in principle in any case. at least in libre.
… which is just what I wrote:
Add enough decimals to the format, and it will show the 9s.
By the way: seeing your localization, this could be interesting to you: [Решено] LO Calc. Вычисления с дробями. Простой пример, странное поведение. : Открытые офисные пакеты. Форум поддержки пользователей
but after all, we are talking about a certain format of cells(Standart;-Standart;; - for libre and General;-General;; - fo excel), and not “by default”. and excel shows right result. but libre - not.
many thanks. this interesting.
If your concern is just formatting (and having that imprecise result under the hood is understood), you might want to ask to change the default number of decimals for the Standard as part of user format - that would be an enhancement request.
Not especially in libre, but in every spreadsheet and database. If you need mor precision check software for math like maple and there are several libraries around to handle arbitrary length calculations. You will never reach perfection with Pi …
.
From times long ago, I remember also BCD-coding, but I don’t think this is an option now.
Youre telling [redacted], it may be inaccurate in principle but on a non-significant and irrelevant Level.
[edit]: so lets rephrase:
your statement: »calculations are extremlely inaccurate« … is extremely nonsense !!!
:[edit end]
( just to remind: the Error happens after ~14 significant digits…
with 14 digits of PI you calculate the circumference of a circle with 1000 km diameter about 0.5 micrometer too small )