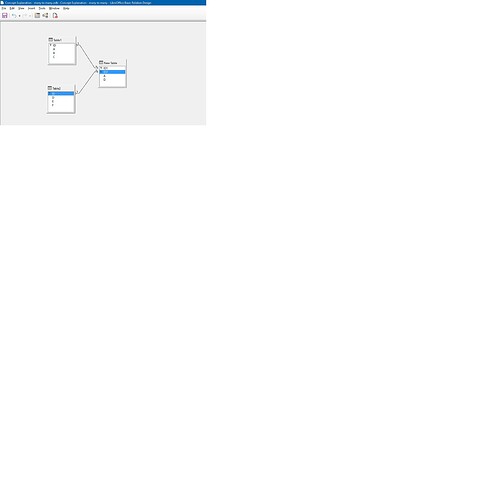
Table 1
A
B
C
Table 2
D
E
F
New Table
A
D
Question: How to…
-
Want to see Data in Fields/columns from Table 1 & 2 (A & D ) in New table
-
data, not just keys’ integers; want to see actual data
-
would like data viewed as table, not query, form , etc.
-
Some reason this was left out : Where A, B, C, D, E, F are fields/columns. in their respective Tables.
-
Creating a many-to-many relationship only results in Primary and foreign key integers being displayed, and not the desired the data fields/columns
Other (response):
- Using LibreOffice Base 7.05.2 (x64)
- Windows 10
Elaboration: Objective is to have a table where the data from A ( Table 1 ) and B ( Table 2 ) can be matched and assigned to one another in New Table, rather then having to create query, form or whatever have you. So at this point in Data View, unable to input and display as desired-required.
example:
New Table
- A (Product)___________D (Use)
- Water________________Thirst
- Water________________Hygiene
- Water________________Digestion
- Soap_________________Hygiene
- Shampoo_____________Hygiene
- Milk_________________Thirst
and so on
Would like to see A and D presented to view data. I agree, this resembles a kludge. But because of constant security breeches, intrusions, lack of legitimacy, support and coopertion, here I am making the best of it. Kludge is putting politely, if one knew or wanted to know a fraction of it. Hopefully changes will aid in explanation. Hopefully images is readable, as it repeatedly reduces its size upon upload.
The interface keeps resetting and leaving things out.
Database:
Embedded Database HSQLDB Embedded
There are few options for simple table creations in Base. Perhaps the problem is being over thought, overlooked ? I have tried to articulate my objective clearly. Yes, table is not created; it is “New”… .as the application is being developed. As for A & D related… .can such not be understood or extrapolated via the crude list, given the shortcoming of commutation available to us? What are we missing ? Thanks.
Challenges understanding and explaining a problem or objective would expected in a learning - assitance support forum, so on, no? Thanks.
Given the objective of the creation of New Table, and populated data presented (as in the crude table I was able to provide), are there not a few possibilities for resolution, or at least road to understanding such? Presented, being in the Table Data View for inputting data.
Surely, as to what is missing or to ensure this data integrity you allude to can be addressed/prevented, can be suggestively addressed rather then in a escalating kludge?
Thanks for now.
Perhaps a solution will come in time.
Light Humor
Thanks, It is a simple enough objective; I am sure you all will be able to come up with a path toward understanding and a solution in time.