Round Down is Rounding Up

English
#6

There are 7 widget models being produced. The mfg. tracks widget completion state in 10% increments.

The bean counters calculate a dollars and cents value for the days total completed widgets.

The completed widgets metric of each model must be rounded DOWN to the nearest integer.
Rounding to nearest or up could result in an incorrect $ value. (We all know that money talks. Even though it can’t sing and dance and it can’t walk.)

Talk with a major financial institution and you’ll probably find lots of cases for rounding down. And likewise, a lot of cases for rounding up and even to nearest. There are valid uses for all of them. Even if we disagree with the usage.

#7

Use this formula:

=INT(726498.789999828*100)/100

#8

Accounting on sheets requires rounding, otherwise you never get a balance due to the floating point arithmetic done in the background. On the other hand, accounting on sheets is a good reason to get fired.

#9

I’m not seeking workarounds. I’m seeking correct operation of the round down function.
Function Wizard
ROUNDDOWN( Number, Count )
Rounds a number down to a predefined accuracy.

The ROUNDDOWN function does not reliably do what it claims. It is flawed. Period.

#10

Not being able to do something as simple as truncating >nth digit is a good reason not to be a sheets developer. It is also a good reason for businesses and professionals not to use LibreOffice Calc.

#14

Hi boss! Who are you? I must have missed something.
Do you know anything about the background, in specific about the relation between the internal representation of numbers and their decimal representation?
Do you actually believe your “alternative software” has no bugs?
Not understanding anything of the kind is a serious reason not to use software.

#15

image
image758×420 33.2 KB

#2

This is a bug. It is related to this FAQ, but in this case, it is possible to improve the calculation (after the rounding, we can simply check if the result is greater than the initial value, and correct it). Please file a bug report on it.

#13

As long as the bug isn’t fixed expressions like

=INT($A$1)+ROUNDDOWN($A$1-INT($A$1);2)

should provide a reliable workaround.

(Ah… There was already suggested a workaround by @schiavinatto.)

#16

@ mikekaganski

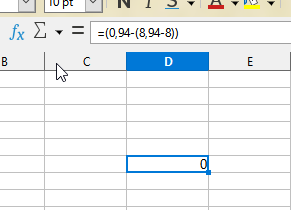
2023-04-14 22-25-38

Win.10 + LibO.7.5.2.2

#18

Fwiw, that’s tdf#154792.

Unfortunately that’s only theoretically.

#17

Looks like a bug, as @mikekaganski also confirms.

Workaround:
Can you use the FLOOR() function instead? It seems to be more reliable(but it is not; disregard my workaround; see (*)). With that, you give the rounding precision as “step size” instead of the count of decimals:
=FLOOR(726498.789999828;0.01)

Edit: I must have overlooked the other workarounds given when I first suggested this. Those other ways are just as good. They all circumvent the seemingly reduced precision used internally in the ROUNDDOWN function, by either moving significant digits aside during the process, or using a different function (or both).
Using the INT() with multiply/divide is the “old school” way which will work in every spreadsheet app known to mankind.
If you need other levels of precision (or dynamic precision) some approaches/workarounds are better than others. It often depends on context and what kind of intermediate results you are working with. Take care not to lose significant value!

(*) please note: I have not tested ROUNDDOWN() vs FLOOR() extensively to determine reliability. FLOOR() seems to have similar issues with other values. Other helpers here have more intimate knowledge of the inner workings and development than I do. See comment from @erAck et.al.

#20

In this case. For the dreaded 8.94-8 case FLOOR(8.94-8;0.01) yields 0.93
(and no, that won’t change).

#21

And Excel does the same :slight_smile:

#19

As explained in tdf#154792, this was intentional, introduced in tdf#124286, and was intended to compensate the normal floating-point inaccuracies, like the previous =ROUNDDOWN(8.94-8;2) producing 0.93 instead of the expected 0.94, because the negation 8.94-8 produced 0.9399999999999995. So the rounding to 12 significant digits was introduced before rounding up/down in commit edcbe8c4e02a67c74ec6f85f28899431dbfa0765 (when the requested number of decimals was less than 12, indeed).

@erAck has improved this in this night’s commit 8186a01f2a26f05645a2a3c9c93b453bd35b796f. All the samples in the report (both OP’s, and my comment 1 there) now behave as expected.

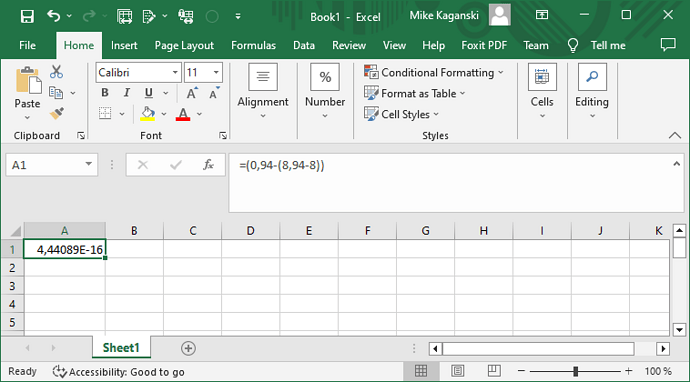
However, it must be noted that the problem can’t be resolved cardinally, because the original problem of tdf#124286 still needs addressing. Despite OP’s claims, Excel also has the inaccuracies, like here:

image
image731×472 37.2 KB

It also rounds up in ROUNDDOWN when appropriate. Spreadsheets, despite being not exact, are widely used in accounting and similar areas, for which they had been tailored extensively; and in these areas, a deviation after a dozen of decimals is usually a sign of FP inaccuracies, rather than a significant information, which has to be accounted for to provide expected value. What spreadsheet software is not designed to is infinite accuracy.

Note also that OP’s claim in the bug:

Microsoft figured it out long long time ago. You’re decades behind on something as fundamental as subtraction and rounding down.

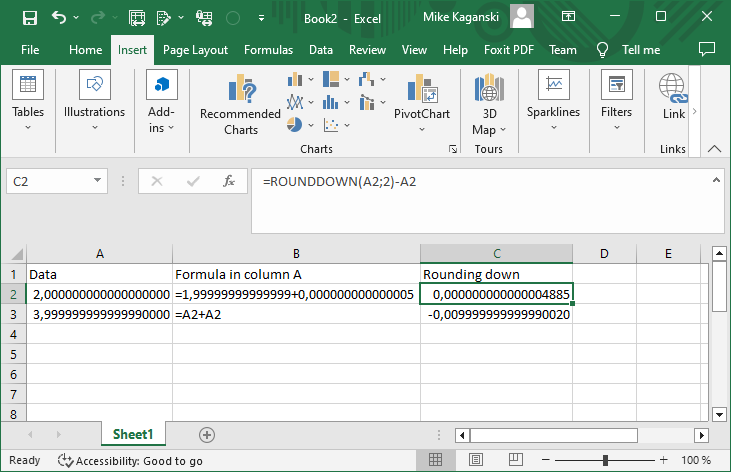
is plain wrong. One can try other examples, where we calculate much more accurate. E.g., having A1:A60 with 0.1 in each, =SUM(A1:A60) would give the expected 6.0 in Calc, but 5,99999999999999 in Excel (one might need to increase shown decimals to see that); and the ROUNDDOWN to 1 decimal on this sum would produce 5.9. Thanks to Dante, who implemented Kahan summation algorithm (or, more precisely, Neumaier’s) in tdf#137679.

Or putting 100.01 to A1, 100 to A2, selecting A1:A2, and dragging down to row 10002 (down to the expected 0) would result in -5,09885E-11 in A10002 in Excel, but 0 in Calc; summing absolute deviations from the correct values in all the cells A1:A10002 would produce ~4,40E-11 in Calc, but ~2,56E-07 in Excel (so total error is four orders of magnitude larger). And thanks to @erAck, this issue is also improved/fixed.

1 Like
#22

What value does Excel round down incorrectly? Give me a value. Not a calculation that returns an incorrect value (ie. floating point error).
Appears you are passing floating point errors into the ROUNDDOWN function and then blaming ROUNDDOWN for the errors.

Like when you cite 0.93 result of ROUNDDOWN(8.94-8,2) on the ROUNDDOWN function. When in fact the ROUNDDOWN function correctly rounded down the value it was given.
The problem in that case is the 8.94-8 subtraction yielding an incorrect value such as 0.9399999999999995 (floating point error). Instead of the correct result of 0.94.
Rounding that value down to 2 digits is correctly 0.93.

#23

Take a look at the screenshot above. It shows which value it passes to ROUNDDOWN. Namely, 1.999999999999995. This value is obtained using a calculation of 1.99999999999999 + 0.000000000000005. And since there is a limit of what the cell can show you, it is checked, that the result of rounding down is larger than the original, by ~5e-15, using the negation.

Simply put: whenever there is ROUNDDOWN(x) - x > 0, the function works incorrectly, according to your definition - no matter how you defined x.

#24

=ROUNDDOWN(1.999999999999995,2)

Excel Result: 1.99
Looks correct to me.

Calc Result: 2.00
Look wrong to me.

ROUNDDOWN(x) - x injects floating point error. ROUNDDOWN(x) is not the issue. The issue is - x floating point error. Akin to the 8.94-8 floating point error (0.93999999999999995).

Stop injecting floating point errors and then blaming the unexpected result on the round down function.

Again I ask. What “VALUE” does Excel incorrectly round down? Give a numeric value. Not an equation that results in floating point error.

#25

OK, you claim that I gave you not a value. I claim that I gave you a correct value, and a correct procedure to validate the claimed error. Moreover, I claim that if you insist that for any given value, no matter how created, the expression ROUNDDOWN(x) - x may produce a value greater than 0, and that is not because of the Rounddown, but because of subtraction, then it is even more severe problem, not a mere correction introduced for very clear and sound reasons, but a plain violation of all fundamental arithmetic rules and also of IEEE 754 requirements, which means that the claimed introduction of the FP error by subtraction can’t be its cause. Then I claim that all this shows that you simply don’t understand what you are saying, or alternatively that you are a simple troll.

One can validate that the values 1.99999999999999, 1.99999999999999 + 5e-15, 1.99999999999999 + 10e-15 form a correct sequence, and their subtraction gives expected results. Further, subtracting the last value from the result of rounddown of the second last gives 0. And there is a UI limitation imposed by Excel, not using and not showing more than 15 significant digits in literals, but no restriction in the values created by calculation.

1 Like
#26

You still have not produced a value that Excel rounds down incorrectly. All you have given are calculations whos incorrect result is fed into the round down function and then blame the round down function for the unexpected result.

And also this…
Yo, The negation of =ROUNDDOWN(1.99999999999999,9) is -1.999999999. Not -1.99999999999999

Again, for the 3rd time, I ask. What value does Excel not round down correctly?

Impressum (Legal Info) | Datenschutzerklärung (Privacy Policy)   Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.