Happened twice, with the same user, in question/291817/.
There is an URL that appears in a comment, and it don’t change the date/time when it appears. First time I doubted of me. Asked user and deleted spam. But now I make screenshots.
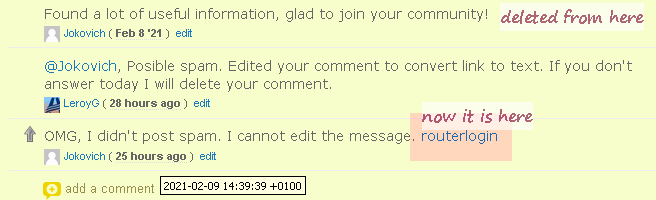
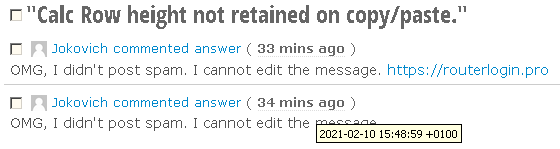
Both screenshots were taken with a few minutes of difference.
¿Some advice?
EDIT: Is there a way to ban users? There is more spam of @Jokovich, and a few more users at Installation on Fedora 14 system fails
I will delete them all (comments).
It’s one of the many problems with this askbot site that many users are trusted to only act reliably based solely on their “karma”. By whatever means somebody accumulated enough points he (f/m) can edit other users posts, or delete them (what I inadvertently did in more than one case - sorry). In case of comments the fact of having been edited may not even be visibly documented.
And there is the strange fact that I can tamper with other user’s comments while my own aren’t eligible to myself for editing or deleting. It may occur that I need to ask someboy else to delete one of my old comments - and he can.
Advice? None. The software simply is unsuitable for the purpose it’s used for.
And: Reading in threads like this one I always am afraid some villain fortunately being too silly to get an idea himself will be hinted to a dangerous vulnerability. This is a similar problem as with software like Windows. There those finding new vulnerabilities are expected to not publish about…
I noticed this technique. Spamming comments is less liable to be detected than issuing fake questions or answers.
But I don’t see the interest of spammers. Maybe they too didn’t understand how this site works: as comments do not bring back the question to the top, the malicious link is less exposed and will likely be less clicked. So, not worth the trouble for spammers.
There are more than 150 user with 200+ karma.
I re-deleted the URL in the comment. This is reflected in my activity as commented answer.
Edit: “150 user with 200+ karma”. None of them was.
Edit 2: I apologize if I am wrong, but my conclusion is that OP (although he denies it) edited the comment later to add URL (or, unlikely, a hacker did it). Date/time is not actualized in the comment, but in the activity.
Maybe they too didn’t understand how this site works: as comments do not bring back the question to the top, the malicious link is less exposed and will likely be less clicked. So, not worth the trouble for spammers.
Or perhaps they are simply looking to gain backlinks
somebody accumulated enough points he (f/m) can edit other users posts …
The edits are still reflected in your notifications; e.g., if I edit commit by @robleyd above, everyone who commented previously would get a notification with my name as “commenting”. So @LeroyG would know if someone edited an innocent comment by that “Jokovich” below the initial warning; so I am positive that there was nothing convoluted, and “Jokovich” is the actual spammer.
That username is known on https://www.stopforumspam.com - used by several email addresses so that’s another indicator that Jokovich is a very naughty boy.