WRITER: Relationship between page margins and other typographic elements

SamSp · November 28, 2019, 5:41pm

I am preparing a complex template for writer, whose layout must correspond to a predefined graphic project, which gives me the height of the body of text, the height of the header, the distance between header and body of text, the height of the footer and the distance between footer and body of text.

I need to know: does the page size as set in [format -> page -> page -> margins -> top / bottom] also include the space assigned to header and footer? If I increase the height of the header [format -> page -> header -> spacing / height] is this increase added or subtracted to the values set in the “margins” tab? And if I increase the height of the header spacing [format -> page -> header -> spacing / height] is this increase subtracted from the height of the header or from the height of the body of text?

In other (and simpler) words: given ct = height of the body of text, h = height of the header, dh = distance between header and body of text, f = height of the footer, df = distance between body of text and footer, which values must I insert in the window [format → page]?

mikekaganski · November 28, 2019, 7:48pm

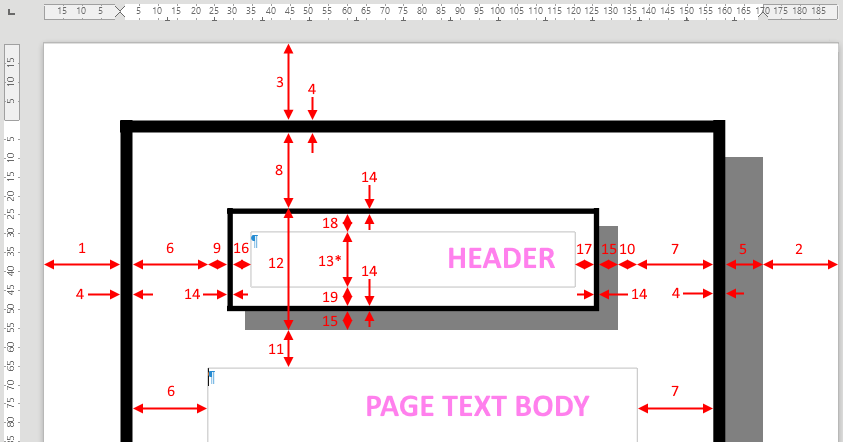
Legend:

Left margin
Right margin
Top margin
Page border line width
Page border shadow distance
Page border padding left
Page border padding right
Page border padding top
Header left margin
Header right margin
Header spacing
Header height
Header text area*
Header border line width
Header border shadow distance
Header border padding left
Header border padding right
Header border padding top
Header border padding bottom

Items 1-3 are set at Page Style dialog’s Page tab.
Items 4-8 are defined on tab Borders.
Items 9-12 are from Header tab.
Items 14-19 are on Border tab of the dialog available by clicking on More... button on Header tab of Page Style dialog.
Item 13* is not defined explicitly; see its discussion below.

Items 4 and 14 are measured in points (pt = 1/72 in); units of other items follow user preferences (Options▸LibreOffice Writer▸General).

Most of the elements are quite straightforward and obvious from the schema and their naming; possibly the not-so-obvious fact needs mentioning that border widths are added to the spacings; and that 12 = 14 + 18 + 13* + 19 + 14 + 15. However, there are two options on the Header tab, that affect items 11, 12, 13*, and need additional explanation, namely:

[ ] Use dynamic spacing
[ ] AutoFit height

When both of these checkboxes are unchecked, the values of items 11 (Header spacing) and 12 (Header height) are used strictly as set. Any content of header’s text area (13*) that doesn’t fit will be cut off.

When AutoFit height is checked, 12 is considered minimal height of the header: if text contents doesn’t fit into 13* that results from the set elements’ sizes, it will expand the height downwards as needed, shifting 11 downwards (height of 11 is unchanged) and decreasing main page text body height.

When both AutoFit height and Use dynamic spacing are checked, then the height of 12 is also minimum, and grows when 13* needs; but when growing, initially it borrows space from 11 (header spacing), thus the total height of 11 + 12 doesn’t change, and main page text body’s top doesn’t move. Only when header spacing is depleted, further growth of 13* (and 12) will start borrow space from main page text body height.

Checking Use dynamic spacing alone doesn’t make sense, and behaves as if 12 is set to 11+12, and 11 is set to 0.

ajlittoz · November 28, 2019, 7:53pm

Only one word: waouh! I’d give +5 if I could, but I’m limited to +1

mikekaganski · November 28, 2019, 8:27pm

I thought it’s worth to share what I learned from trying to improve our interoperability with Word in this area, where our layout is very different from Word’s (to the extent that some layouts possible in LO are totally impossible in Word, and vice versa) … Glad you find it useful!

ajlittoz · November 28, 2019, 6:45pm

In Writer, contrary to Word, page margins define an absolutely-no-print area. No element (apart from manually positioned frames) will ever be laid out in the margins.

The remaining area in the page is shared by the header, the text body, the footer and spacings between there elements.

h + dh + ct + df +f = page_height - top_margin - bottom_margin

Use this formula to compute the value for the top and bottom margins. Also, in your page styles, make sure boxes AutoFit height and Use dynamic spacing are unchecked (Header and Footer tabs) so that your paragraph styles and spacing height settings will dictate the dimensions without adjustment by Writer.

To show the community your question has been answered, click the ✓ next to the correct answer, and “upvote” by clicking on the ^ arrow of any helpful answers. These are the mechanisms for communicating the quality of the Q&A on this site. Thanks!

In case you need clarification, edit your question (not an answer) or comment the relevant answer.

SamSp · November 28, 2019, 7:01pm

Wonderful answer, but I does not have enough points to upvote. Thanks.

regs1 · April 5, 2023, 2:05pm

So in Word you can explicitly set page body margin for all pages and forget about it. In Writer you have to sum 6 different numbers to set proper margin for every side of every single page to make sure that the document comply to a standard. It’s not usability, it’s a mess.

mikekaganski · April 5, 2023, 2:09pm

Does your standard say “use this margin, and don’t care about what’s on it”? If you do not use header/footer/border, there’s no difference. If you use, the standard will define their dimensions anyway, and you will consider those in your other software, too, just in different places in the UI, so no difference in complexity.

regs1 · April 5, 2023, 2:18pm

Most standards around the world explicitly define body margin. Headers, that might include references and especially page numbers, are located outside those margins. So the standard says the margin is 1 cm from the top. In Word you have direct control of that number. In Writer it’s not the difference, it’s complete lack of ability.

ajlittoz · April 5, 2023, 2:43pm

No, it is a matter of correctly defining what a margin is. In typography (which IMHO is a much better reference than M$ Word), a margin is a no-print area (except perhaps for what is called marginal notes). With this understanding Writer is closer to tradition.

What is surprising in your rant is you focus on top and bottom margins only, forgetting left and right margins where we meet the same dilemma.

I deduce that you don’t use styles. Styles give you a tremendously powerful control on your layout. You set the geometry (layout) for all paragraphs, pages and frames and you forget about it: you just apply a style when you need it (a double-click). And when your styles are designed (or provided if someone else did the job) with “standard” in mind, it is a real pleasure to write. You forget about the “standard” pain thanks to styles.

Unfortunately very few users read the Writer Guide and even less Bruce Byfield’s excellent Designing with LO available at the same link.

regs1 · April 5, 2023, 3:48pm

Standards, a law, define what margin is. Not personal traditions. There is a reason why Word was designed to separate headers/footers and the body. That is because most standards define explicitly the body margin. For Writer it’s just about the way to do different, own way.

Headers and footers are on top and bottom, so left and right margin are just less vulnerable to the problem.

It’s not what can be called usability.

Unfortunately it’s been long time since Document Foundation haven’t heard users and read standards. A bug ticket 33304 has been there since 12 years. When a user want to create a document he want to do it quickly and reliably. A user doesn’t want to spend time to design and calculate.

ajlittoz · April 5, 2023, 4:07pm

Then styles are the ideal tools for that. Using styles styles is quick and guarantees reliability.

Unfortunately you can’t use a powerful, thus complex, application without investing some time in reading documentation. You certainly read some time or another M$ documentation. Don’t tell me using Word is “intuitive”. “Intuitiveness” results from routine use.

Only one-shot dependable documents can be written quick’n’dirty where you don’t mind deviations from “standards”. Any document intended for medium or long term requires a design step. But you design the layout only once, so computations really don’t matter.

Regarding the header/footer issue, the difference between Word and Writer is only a constant offset. It is very simple, not needing complicated arithmetics, to the point that the import and export filters can make the conversion automatically.

Once again, this difference becomes bothering only if you tune your layout manually with direct formatting (and you may be “polluted” by M$ Word because this is the only way to do it there because Word has no notion of styles beyond Paragraph ones and forces you to manual formatting).

Word has its own idiosyncrasies for sure: how do you tune the distance between the top edge and the header? between the header and main text? What happens when your header needs several lines and would require a change in the margin height? All these issues are nicely managed by a page style.

But you are free to manual format everything and face tuning difficulties.