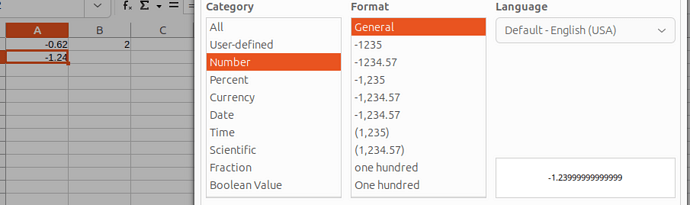
Are you sure? Which is the cell format? What happens if you set it to 0.0000000000E+00? Reminder: this does not change the value, just how it is displayed.
from this point on we disagree. A.) there are native decimal CPUs, IBM, B.) what binary CPUs calculate depends on the numerical system / datatype you use, C.) there are qualified decimal systems available.
yes…available in theorie, but in practise they are 5 to 10 times slower than good old double-precision-foating-point algorithms!
And they won’t solve all cases: if your arithmetic value is not a strict decimal one, you’re back to the problem. Unfortunately there is no perfect solution to this arithmetic problem. It is a matter of primality and you can avoid it.
maybe, however that doesn’t harm a spreadsheet in any way, the bottleneck are users and display. No user realises if a recalculation lasts 0.2 microseconds or 1.0, and in output - on screen - decimal formats beat binary up to 1:10, in a very costly operation. Add two values in bin64: 6.9 CPU ticks, dec64: 92, read in 0.9999999999999999 in bin64: 283 ticks, in dec64: 105 ticks, print out 0.9999999999999999 from bin64: 788 ticks, from dec64: 36 ticks.
What does Calc do when a user changes a cell? Recalculate the chains dependent on that cell, and printout some ~300 cells on screen. Evtl. prepare some 8, 24 or 48 times more around the display frame for faster scrolling.
Estimate which datatype serves better.
Just ask users what they would prefer? Having some number crunching calculations a little slow ( let’s say I tested a testsuite without! output to 600 instead of 350 seconds ), with decimal correct results, or quick with most results “a little off”, and some completely nonsensical.
Yes, admit, however A.) do come near to what users are used to, enable man - machine harmony, !PREDICTABILITY! what the results will be. And B.) nobody forbids hybrid models which - with some more effort - serve a mode by users choice.
The evil is pretending “decimal” while not sufficient, the second evil is not to tell the users in advance, the third evil is to ignore decimal datatypes because “slow” ignoring their capabilities and options to improve, the fourth evil is to wrongly tell users - or me - decimal would be impossible.
Let me throw in a real-life analogy: You have several ways to get from one floor to another. If you can fly like a butterfly, you’re an alien. Your feasibility is therefore limited. Using stairs and a ladder, you move digitally step-by-step; using a rope and a slide, you move analogically. With the latter two, you can assume any intermediate position, something you’ll never achieve with the first two, no matter how many smaller intermediate steps are integrated. There will always remain those “non-tolerated” areas in between that can’t be clearly assigned — not even with hysteresis feedback. Fuzzy topology was invented as a helpful solution in the multi-stage digital realm…
All those problems and therefor much more are inherent in every topology of hardware A/D- and D/A-converters. We can decide whether their inaccuracies are tolerable or not. If the salesman dictates a cheaper model, then we engineers have to do hypocritical gymnastics to avoid accepting such large deviations, often with some kind of fatal consequences at some point.
@koyotak: this will be my last comment
When using a tool, you must follow its usage rules. For instance when driving a car, law tells on which side of the road you must stay. If you viloate the rule, you’re in danger.
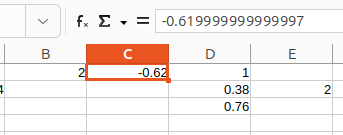
In your case, the difference between 0.62 and 0.619…77 is 3 10^-15, i.e. in relative value 5 10^-13. Such a tiny difference is negligible in most practical situation.
I agree with you that a human prefers to read 0.62. This is the role of cell format where you specify how many digits you want to see and Calc will do the visual rounding.
This is for general-purpose calculation. You are in an accounting context. This context also introduces rounding conventions (not truncation). This rounding is necessary every time you multiply or divide to reconcile what you (want to) see and the value kept in the record.
To do that, I systematically write =ROUND(…; 2) around accounting formulas involving multiplication and division. By doing so, I make sure that the value shown is exactly the same as would be used in later calculations. To avoid “cent errors” (as can happen if you SUM() “raw” values and in parallel rounded values, you must follow a strict discipline where you chain only rounded intermediate values, not recomputing them every time you need them (this means your formulas in the end are extremely simple because you store in separate cells scratch intermediate values when they have an accounting sense).
The discrepancy between displayed and “mental” value occurs whenever you have a fractional base in your floating-point number representation. Even if you have a decimal floating-point unit (base 1/10), the fact that the distance between two successive stops in the numbering set is proportional to the number order of magnitude. Thus the scale is quantized with a variable step. You can’t avoid this if you want floating-point, i.e. a huge range.
Old business computers had decimal arithmetic. But this arithmetic was integer-based, not fractional. Since this was used for accounting, floating-point was not necessary. You only had to keep track of where the decimal point would end up after an operation. It is not complicated but requires programming. This was entirely handled behind the scene by COBOL or PL/1. Spreadsheet are not programming languages and try to provide an easy interface to simple tasks. However, every user has his/her own original purpose. This can’t be accounted for universally. This is why TRUNC(), ROUND() and other functions are provided to fulfil th specific needs.
If you want some insight about the issues with fixed decimal and floating-point arithmetic, I encourage you to read Donald Knuth’s Art of Computer Programming, Vol. 2, Semi-numerical Algorithms.
I remember having read an algorithm for outputting a floating point number and avoid printing senseless digits like the final …99997 above. It tried to decide whether the last bits of a number where meaningful or not. This seems very appealing but I lost the reference. It could have been from some IEEE Proceedings or an ACM publication.
It is on-topically! To better understand and comprehend the brutal, real and very complex world. Without wanting to discover the mythical formula of how our world is composed.
Yours tiny peephole offers a brief impulse to plunge deeper into the intimate stratosphere, which a technician must often painfully endure the more experienced they become, fleeing the swamps of all theories within the atmosphere.
Just to gain that microscopic knowledge of how large the iceberg beneath the water’s surface can even be, which the theoretical teacher fails to even hint at. Training courses and universities are far too intellectual. How often have I had realized that their theories were, at the workbench, figments of my imagination. Example: Why do I need the 6th decimal place of pi when the circle drawn with chalk on the blackboard already has an unstructured width of several millimeters thanks to the rough surface of the blackboard? And what does the jigsaw do to the wooden board, no matter how precisely I try to guide it? Or: How can I dictate to the PCB manufacturer via e-CAD that such-and-such a trace must have a width of 7 μm, without knowing how much the chosen PCB manufacturer will underetch or overetch, thus transforming the ideal rectangular cross-section into a rounded or square surface? Only to discover during electrical testing that the distance to the adjacent copper trace has critical points. As a technical illustrator, I experienced countless ups and downs and was impressed by the heights from which academics looked down on me, or up to me, a non-academic. I was also impressed by how important the displayed millivolts of the mains voltage of a multimeter display were to electricians! Which inspired me to research the tolerance ranges of all.
Even the cheapest of calculators is able to give correct results of addition and subtraction.
Even the builtin Microsoft Windows calculators can give the correct results.
Even old clunky desktop adding machines of bygone eras give the correct results.
Yet here we are in 2025 and spreadsheet developers/engineers/programmers can’t give correct answer of 1st grade subtraction.
Applying the ROUND function to every subtraction to get correct answer is pathetic. Computers can do that to accommodate humans rather than humans accommodating computers.
Everybody knows the precision of addition/subtraction is equal to that of the most precise operand. Program it. i.e. accommodate humans.
It’s funny, Microsoft engineers can do it with the calculator, but not with Excel.
Maybe the Microsoft engineers use some rounding in the Calculator BY DEFAULT, but not in the Excel.
YOU must use rounding functions in the Excel - if you need them.
Frequently asked questions - Calc: Accuracy problem - The Document Foundation Wiki
calc: rounding: general precision problem?
calc: are decimal correct calculations possible?
Unexpected decimal precision error in Calc
etc etc
128312 – Calculation involing some decimals return incorrect floats with 12 d.p.
The decimal point is the cause of the calculation error! So =4595–4657 correctly yields –62.00000000.
Oh your understanding is growing … slowly … binary integers are perfectly suited to substitue decimal integers … substituting decimal fractions by binary fractions is not, many become “endless iterations”, need to be shortened, rounded, often rounded again after operations, and that sometimes fails ( from a decimal POV ). Also pls. look up “evil cancellation” why this more often and more significantly harms subtractions than additions.
There is a little terminological problem.
“Integer” should be understood as a mathematical term. This way there neither are “binary integers” nor “decimal integers”.
In what way we prefer to represent an integer number when writing on a blackboard or when designing an FPU is a matter of tradition or a technical decision.
Currently an ordinary FPU has a maximum of 53 dyadic digits (bits) of which the first one isn’t stored because it isn’t significant (always I) due to normalization.
Anyway the largest integer that can be exactly represented this way is
IbIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII * 2^52, and the question whether this actually is to be interpreted as an integer or as a rounded dyadic fraction with more than 52 digits behind the dyadic delimiter b (regarding the dyadic exponent) can only be answered based on the context.
FPU register content I * 2^99 may or may not represent an integer. Donno.
In short: For a current FPU and for any practical purpose 52 significant bits are enough precision, and relative rounding errors in the range of few*10^-16 can simply be tolerated.
sorry Lupp, I just wanted to keep short because again contenders start to complain about trolling … “binary encoded integers” and “decimal encoded integers”, and surely only in the range both versions are precisely representable. The big difference is to fractions , where binary encoded decimal fractions inherit special properties which make calculations difficult … as we both know …

What is tolerable I disagree, one can deal with small deviations, exponential explosions become difficult.
For everyday use an integer is simply a floatingpoint fraction with a sufficiently large order of magnitude. If missing (not in register) digits would all be 0 or if some bits at the end of the queue are only present due to small errors in preceding calculations we cannot know.
Use a CAS if you need one. It may (again limited, of course) be able to perform algebraic and numerical (with fractions) reductions without any numeric error, and deliver an appoximative decimal fraction in a last step if ordered.
If you feel capable of higher level programming, create an interface between Calc and Maxima/gnuplot. 
heeeyyy!!! don’t trigger me into trolling … you are upsetting your colleagues … if … and it might be it already happened … I’d like to improve a spreadsheet, or … if … and it might be it already happened … I’d like to use a spreadsheet with ( limited ) decimal capabilities … I’d choose Gnumeric in the decimal64 variant. A clear codebase, decimal available with one parameter in compilation, compiles in some seconds where LO Calc AFAIR used 30 minutes … quicker in use for nearly all functionalities except conditional formattings …
You may have noticed that I stopped posting here or contributing to Calc years ago. That was not only because of Mike Kaganski’s unpleasant “tone,” but also because I simply liked Gnumeric better. While 20 developers here spend years tinkering with tiny problems, and asking if they have vanished by chance the one year or thr other there one! maintainer goes into business and integrates decimal datatype within 8 weeks… I am eternally grateful to the guy who suggested somewhere in a bug report to adopt Gnumeric’s math engine. Without him, I might never have found it.
So, as far as I’m concerned, I’m not trolling around here anymore, but if I get too annoyed with mocking comments, there will be answers.