hi @all,
!!! Caution! this is ‘in progress’, and I just noticed errors where I have to sort what are thinking errors of me and what are inadequacies of calc or tools (rawsubtract), see comments, I will adjust the question and example sheets based on my progress, sorry, maybe I started the discussion too early, but I need it - the discussion, and the results so far look so good that they certainly still have errors, this is normal, but probably will not fail completely … !!!
there are a few - imho too many - questions on the internet ‘why doesn’t my spreadsheet calculate correctly?’
a few of the ‘classics’ are:
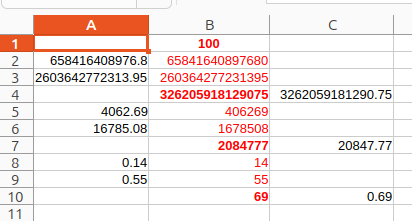
'=0,1 + 0,2 ’ results in 0,300000000000004 instead of 0,3,
‘=1234,12 - 1234’ results in 0,119999999989100000 instead of 0,12 and
‘=0.043 - 0.042’ results in 0.000999999999999400 instead of 0.001,
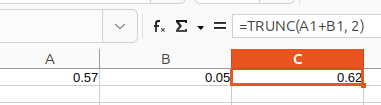
attached is a sheet which calculates (more) correctly with a few primitive tricks, I would be glad if people with knowledge of the matter would have a look at it,
sample sheet, click for download
[edit - adding another version of the sheet, added a macro formula for calculation, and saved in tdf 1.2 extended format]
sample sheet with macro and in 1.2 format, click to download
i hope i included all neccessary macro help functions …
[/edit]
mostly such questions are answered with ‘that’s how floating point maths is, but it’s fast’, ‘learn first what that is (floating point mathematics)’, ‘it must be like that’, ‘we can’t change it’, ‘look at Weitz (www.weitz. de/ieee), “the error is correct”’, ‘ex$el calculates the same way’ and so on, the claim that a spreadsheet should and could calculate as ‘correctly’ as we once learned it in school is simply negated, either with ‘impossible’, or with ‘performance’,
I find this after 35 years of standard (IEEE 754) and 35 years of development (of LO calc) ‘a bit weak’, so it gets on my nerves so much that even comments like ‘spam’, ‘ignorant person’, ‘your pet peeves’ etc. didn’t deter me to think about it,
I think at least many of the problems ‘work better’, and users should be allowed to get real results even if they are different from ex$el,
attached a sheet what shows that, red marked: wrong, green marked: better,
I don’t say that this is one or ‘the!’ final solution or ‘the last word’, but it is a clear proof that:
- for many cases better results are possible,
- they can be achieved with relatively little effort,
- for the users much more comfortable and
- are much less error-prone than if the users always have to stumble over errors first and then have to manage the rounding themselves after recommendations for workarounds,
I would like to have an open discussion about whether it would be better to implement such calculation - at least as an option - in calc, and if not then why not,
in this discussion could be discussed / clarified among other things:
-
that there are completely different problems if decimals do not (can not) exactly match the IEEE binaries in which they are mapped, in contrast to the fact that certain calculations are difficult (cancellation in subtraction and absorption in addition), this is often ‘lumped together’ even by ‘professionals’, which hinders suitable problem solutions, the first is relatively painless, it’s just the way it is, and does no harm as long as the ways to (to binaries) and back (to decimals) match, ‘cancellation’ on the other hand can inject significant! errors, but you can ‘calculate out’ most of them !!!if you do it right away (on the intermediate result)!!!,
-
that these errors may be marginal, but make significant differences e.g. for comparison operations (=?, >?, <?) and cause wrong results for MOD, number series, downfills etc.,
-
whether it is right to fight the errors with ‘arbitrary untargeted rounding’ which in my opinion causes errors in other places, and rather bigger ones,
so … I am happy to receive opinions, and also criticism …
reg.
b.