?
By the way: “decimal calculations” by pencil & eraser were made by truncation.
I’ve seen small inventories for the yearly balance being computed via desk calculators, pencil & eraser (literally).
[Quantity x “cost $”] →discard figures after ,nm (the cents). Cross them out.
Idem for, by hand, say ⅓
x |____ ←(3 here)
… do it up to ,__ and stop.
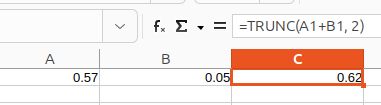
Sorry, copied from wrong row or typo, try 0.54 + 0.57, Calc will display 1.11 and trunc to 1.11, however that’s combining faked display for IEEE result 1.1099999999999999, and “fuzzy rounding” with a 4 bit? “snap to zero”. Here working correct, but try to estimate how long it will hold. Or memorize the already mentioned “There is nothing exact in floating-point calculations in Calc, …”, Mike Kaganski 2023 in “comment #5 in Calc Round Down is Rounding Up for some values”, * [Online]. Available: 154792 – Calc Round Down is Rounding Up for some values, retr: 2025-05-13, mentioned in C#54 here, and evaluate the title of that thread reg. reliability of trunc ( which is rounddown direction 0 ).
My approach here tries to be the practical use of Spreadsheets (here = Calc of course), not a theoretical one.
So users must be aware of floating point arithmetics. For e.g. Accounting, employ TRUNC according to local currency.
For other professional fields, also the user (we Engs. etc…) must employ the tool (Spreadsheet) accordingly.
Yes: perhaps SO sophisticated softwares in XXI Century could have a “type” like a true “decimal(_, n)” – no roundings at all. But I’m not able to argue about that (?)
second that.
LibreOffice comes with a database component supporting dozens of database engines where this is a matter of course.
In your sample document, you are rounding the result of subtraction to the position of 15th decimal digit of the greater of the original values. So your idea is to limit the precision of calculation to “fix” catastrophic cancellation.
Your idea is not new; also it is not correct. Your idea is about assumption that what is displayed in cell is closer to “ideal” value than what is actually there. It might be true only with very limited set of cases, where the values in cells are manually typed there by user, and only addition/subtracted is used.
But it would make most real calculations worse. Consider any trigonometric functions where you use radians, or any logarithmic functions, or even simple multiplication/division. There you get more “significant” digits than were in initial numbers that user had entered. And arbitrarily limiting the precision of those numbers would result in much worse catastrophes universally.
For instance, take this simple calculation of well-known triangle and its scaled variant:
A B
1 3 =A1*PI()
2 4 =A2*PI()
3 5 =A3*PI()
4 =SQRT(A3^2-A2^2) =SQRT(B3^2-B2^2)
In ideal world, A4 must be equal to A1, and B4 to B1. In Calc, although the value of PI() is naturally imperfect, RAWSUBTRACT(B1;B4) also shows 0. But if in B4 we replace SQRT(B3^2-B2^2) with your SQRT(ROUND(RAWSUBTRACT(B3^2;B2^2);15-MAX(ROUND(LOG(ABS(B3^2);10);0);ROUND(LOG(ABS(B2^2);10);0)))), we suddenly get the difference between B1 and B4 by 1.77635683940025E-15.
Carefully prepared limited-precision input in your sample is not representative. Note that I don’t talk about performance here, I only talk about precision that you try to achieve. Your approach would fail miserably in all but simplest cases. Current implementation of subtract is of course not ideal (in this non-ideal world), but you may notice that it still tries to be reasonably smart using rtl::math::approxSub which handles near-zero result (unlike the implementation of RAWSUBTRACT, which tries to be simple).
hello @mikekaganski,
thanks for your help,
rounding acc. the greater operand may be wrong, acc. the smaller may be better, it’s experimental,
i just stumbled over 29,999999999999900000 if i wrap rawsubtract in a macro:
function rawsubtract_a (ByVal darg1 as Double, darg2 as Double)
oFunctionAccess = createUnoService( "com.sun.star.sheet.FunctionAccess")
rawsubtract_a = oFunctionAccess.callFunction( "RAWSUBTRACT", array(darg1, darg2))
end function
and call ‘=RAWSUBTRACT_A(33,0000000000001;3,0000000000001)’,
i used it in an attempt to stay away from 4-bit truncations and similar, will try to improve,
it’s a general problem being limited to use imperfect tools to improve just these tools …
‘trigonometric functions’: yes, but:
- the average user wants correct subtractions first,
- the fail may result from other shortcomings than my idea? see above,
- I don’t refuse to improve my idea, I just refuse to carry on too glaring errors in calc,
my samples are targetting ‘massive cancellation’ when subtracting similar values,
@mikekaganski’s sample deals with values with significant difference,
adapting the formula to apply less tight rounding to ‘more different’ values should be simple …
as - perhaps that’s a good idea - don’t touch integers?
in the end it may require a ‘case differentiation’ between ‘one operand zero’, ‘addition’, ‘subtraction of identic’, ‘subtraction with very small difference’, ‘subtraction with small difference’, ‘subtraction’,
why not, progress justifies some effort …
the performance part will come later, it is! important, i think i can! solve,
‘trigonometric functions’: yes, but:
- the average user wants correct subtractions first,
No. Please write “I want that first”. It’s the usual thing, that you claim something to be general rule when you have no idea about demographics of usage of the product. There’s no “But” here, it must be correct everywhere.
- the fail may result from other shortcomings than my idea? see above,
Absolutely unclear what you mean.
- I don’t refuse to improve my idea, I just refuse to carry on too glaring errors in calc,
There’s nothing to discuss until there’s an idea. There is clear understanding that what you ask is generally impossible, among those who have substantial knowledge in the topic. You insist on “it must be possible, I don’t believe you, I’m not listening lalala”. Ok, that’s fine, but that’s your task to come with the viable idea. You came with something that is absolutely old and wrong; I took time to explain why. Up to you to come with something else.
There’s a general rule: extraordinary claims require extraordinary evidence. Your claim (“there is some method to make it perfect or at least generally better using IEEE numbers”) is extraordinary one. It doesn’t mean it’s necessarily wrong, (although I’m sure it is) but it needs extraordinary proof. E.g., a great analysis which would prove it’s (more) correct in general case, or that tests the whole range to confirm that claim. Yes, testing square of 4 billion possible numbers (to at least prove it for 32-bit float case) is impossible. But then at least use some possible number of uniformly spread numbers, and make an analysis on those.
-
you’re right, rounding results makes sense with ‘round’ operands, and may harm ‘special values’ (besides that the accuracy you use is outside the ‘15 digit range’),
-
importance of targets … imho 95% of calculations with calc are accounting and similar, less than 5% of users will use pi() or similar anywhere,
-
my wish: fulfill both! targets,
-
in an attempt to decide where to round and where not and to use ‘-’ as you said better than rawsubtract i stumbled over an old problem:
@ajlittoz: i doubt in calcs “correct math” (over the subset of Q …), try following calculation:A1: =22
B1: =63,999999999999+A1*10^-14
C1: =-63,999999999999
D1: =A2+A3
E1: =RAWSUBTRACT(A2;-A3)
vary A1 between 30 and -30 and observe results in D1 … other people had a similar wish - correct math - and to achieve that for some special cases (result ‘0’) they äh … (brutally raped?) … calcs precision … is there any option to switch that off?
imho 95% of calculations with calc are accounting and similar, less than 5% of users will use pi() or similar anywhere,
Ah that “imho” again. But if your estimation is correct, then LibreOffice is perfectly fine for most of its userbase as is, otherwise they wouldn’t use it there. Your changes would benefit no significant percentage of userbase, and will hurt most (even if you invent something working).
rounding results makes sense with ‘round’ operands
There’s no way to know which operand is “round”. The very idea is flawed. The problem you try to workaround is exactly that the numbers have some data in any bit of its mantissa, and there’s no property that could tell “round” numbers from “special”. Even trying to count zeroes before the tail in decimal representation would fail, and break deliberate operation with small deltas.
@newbie-02: what are A2 and A3 in your sample?
Anyway, I won’t try your sample. Adding numbers which differ by 14 orders of magnitude is bound to give inaccurate results. 14 orders is ~46 bits. When the mantissas are scaled before addition, only ~10 bits remain is shifted A1. This means shifted A1 is known only to ~1/1000=0.1%. What do you expect with such a loss of accuracy?
This is what mathematics tell you when you take into account IEEE-754 specification.
I unfortunately lost the reference to an algorithm dealing with such a case (huge difference of order of magnitude between numbers in addition/subtraction). The algorithm proceeded by careful order of operations. You pay the improved accuracy (but not exact mathematical precision) with an increase in computation time.
sorry, i failed in numbering:
A1: =22
A2: =63,999999999999+A1*10^-14
A3: =-63,999999999999
A4: =A2+A3
A5: =RAWSUBTRACT(A2;-A3)
vary A1, observe A4,
“There’s no way to know which operand is “round”.” - 0,5 0,25, 0,125, 0,1 : round, pi() odd, 0,07 should be round, but calcs ‘specialities’ makes it difficult for me to calculate,
“and break deliberate operation with small deltas.” - but that’s exactly what was done with the 4-bit cut, and it bothers me immensely … the sample above is a try to show that …
for every try to triage between meaningful content and fp-artifacts i need to get a handle on it, that’s blocked in calc 
“There’s no way to know which operand is “round”.” - 0,5 0,25, 0,125
These numbers are already “round”. So they need no more rounding. The text was: “rounding results makes sense with ‘round’ operands”, and I assumed that the quotes around ‘round’ meant that you talked about numbers that are close to round. If you have truly round operands, you need no rounding of results. If your operands are not round, as in 0.1, you can’t tell if they are supposed to be round.
I unfortunately lost the reference to an algorithm
@ajlittoz: tdf#137679.
@mikekaganski: Thanks, it was indeed Kahan algorithm.
@newbie-02: you don’t put yourself in the correct math context. You stay in the assumption that the radices are 10 and 2 (integer radices) which is what we are taught in college classes. The hardware truth is the radices are indeed 1/10 and 1/2 (fractional radices) and the story is totally different. It is impossible, except for rare cases, to convert exactly from one base to another one. It is a matter of primality. Read Knuth for mathematical details.
All you can do is to exchange the hardware idiosyncrasies for smart chain calculation. Your sample dives head first into the traps: once you computed A2, you can no longer compensate. You lost A1 precision and anyway it is likely that the result of the addition does not exist in the IEEE-754 subset, needing therefore a rounding to a close element (up, down, closest, furthest, zero, infinity whichever mode is in effect).
hello guys, let me once again say i thank for your help!
and please stay with me a little further …
- ‘rounding’ - i didn’t want to round 0,5 any further, i want to check if i have operands as such and then be sure that a rounding of the result doesn’t harm,
- ‘the computing of A2’ is ‘not so bad’ (one might discuss the rounding for x5 in A1), bad is the result of the calculation in A4, ‘weitz’ can do better, ‘rawsubtract’ can do better (see A5), calc can compute 16 digit resolution outside the range -/+ 22 in A1, precision is not! lost in ‘IEEE’ or ‘doubles’ but in calcs implementation of subtraction,
- ‘It is a matter of primality’ - won’t say it’s trivial but i know about such, about 80% of 1-decimals-digit figures lack enough '5’es in the enumerator to cancel out the '5’es in the enumerator, and already 99,84% of 4-decimals-digits, they stay ‘odd fractions’ for binary representation and become ‘endless’ …
… continued in next comment …
continued:
- another point is if calc actually uses my / the FPU? @ajlittoz wrote about ‘80-bit’ and i’d read it in plenty other places …
the multiplications 0.07 times 10^17 (7000000000000001.00) and 0.07 times 10^16 (700000000000000,1250) give ‘strange’ results,
this evolves from the rounded up representation of 0.07 with ~111101100 at the end of the mantissa (~111101011 | 10000 is cut off at the “|” and rounded up because of the following 1), so far understandable, but with a FPU that calculates with 80 bits the error should occur - if at all - much further ‘behind’ and the result should be clean in the 52nd bit … according to what weitz calculates in 128 bit mode, there ‘rounding up-1’-es occur, but only in the last of 112? bits … calc produces results as if such is affecting bit52???
@mikekaganski: you’d write ‘Your idea is not new; also it is not correct.’ … do you remember if there are any discussions about it i can find on the web?
and … for me it looks promising how many of the ‘classic fails’ could be solved that way, of course something would be good to ‘not harm’ meaningful other values, i do! have an idea
even if it was tested in the past and didn’t turn out useful … some things have changed, calc’s rounding is far from good but better than in the past, you found a better math library for ‘string to double’?, hardware performance exploded … i like to give it a new try …
perhaps - that’s a proposal - some of the ‘tricks’ implemented in the past (to cover weaknesses?) as 4 bit truncation, shrinked display for fractional values and so on, are now obsolete and c/should be undone? see e.g. calc: wrong calculation? would like a recheck, …
What makes me feel that your effort is wasted is the fact that you seem to ignore that what you try to do is a thoroughly developed math science, with proofs of the theorems etc. It is explained in the well-known Wikipedia article, and you must realize that before you come with a brilliant idea, in such a practical field having vast amount of intelligence put under strictly scientific approach, you must master the science behind it. So what you do again and again is plain wrong: without mastering numerical analysis, you waste time. You resemble the inventors of perpetuum mobile, who keep sending “inventions” claiming to break thermodynamics, and the scientists who (unlike me) value their time, just have a templated response to such claims, sent without reading.
