So $X$2: instead X2:?
… and $X:$X. 
Now it remains to write the same thing in RC-notations and the question can be considered closed
{=IF(RC[-1]<4;-1;MAX(IF(MOD(RC[-1]; ROW(R2C:INDEX(C;SQRT(RC[-1]))))=0; RC[-1]/ROW(R2C:INDEX(C;SQRT(RC[-1]))); -1)))}
My initial plans also included speeding up the formula by 4 times, discussing whether rounding is necessary for large argument values…
But it’s all up to the author of topic.
I’m late once more, and I have to admit that I probably didn’t study all the previous posts thoroughly enough.
But there is one question I would like to ask the original poster:
Why do you search for the largest proper (<>1, <>TheNumber) factor contained in the number? It’s the co-factor of the smallest one. Trying a solution with the help of tests, it’s clearly adavantageous to start with small divisors, and in many cases testing will end with 2, 3, 5, or probably 7.
In the following form it will handle numbers up to 4398054899715:
=IFS(RC[-1]<4;-1;ISEVEN(RC[-1]);RC[-1]/2;1;MAX(IF(MOD(RC[-1];(ROW(R1C:INDEX(C;SQRT(RC[-1]/4)))*2)+1)=0;RC[-1]/(ROW(R1C:INDEX(C;SQRT(RC[-1]/4)))*2+1); -1)))Indeed! @andy-andyo , please clarify - what numbers will you be dealing with? If we know the upper limit, the maximum number, we can optimize the formula. And now we are all carried away by dividing the sample into insanely large numbers, and our formulas for large test data hang Calc for several minutes.
ref - handle numbers up to 4398054899715
16/03/2023
hi - gradually catching up and realizing I did not answer half your questions. My spreadsheet is handling only 1000 rows at a time. Whilst in reality the numbers input into the spreadsheet will be random numbers - not in ascending or descending order - I am however testing with blocks of 1000 numbers from the Number Line that are in ascending order. I personally have no limit on the size of the numbers in the 1000 block. The computer has the limit. Andy
Yes, you’re right, a computer in this sense is much weaker than a person - it is not a dreamer, it is a pragmatist. As @Lupp already pointed out, Calc can’t exactly represent a number larger than 2^53-1=9007199254740991=nine quadrillion, seven trillion, one hundred and ninety-nine billion, two hundred and fifty-four million, seven hundred and forty thousand, nine hundred and ninety-one. To simply find out if this number is not prime, you need to check its divisibility by every odd number (or each prime number) up to 94,906,265 … Quite a difficult job, but Calc can handle it - just need to come up with a not very complicated way to make him do it. For information: even if we fill the table column from beginning to end with consecutive prime numbers, all 1048576 cells, then we will only get to the number 16290047. And this is only enough to check numbers up to 265,365,631,262,209 inclusive. In other words, nine quadrillion is still a long way off. Therefore, the advice to abandon Calc and use a specialized tool seems very reasonable.
NB This very large number 2^53-1 is not prime, it is the product of three prime numbers 6361*69431*20394401
Okay, let’s try this approach.
@Lupp, thanks for the tip - indeed, working with prime numbers is much more convenient than iterating over all the row numbers in a column.
So, we use Lupp’s idea - we look at the remainder of dividing a given number by each “known” prime number. As soon as we meet the remainder of the division equal to 0, we divide the original number by the found prime number and get the largest divisor.
Where to get prime numbers? Of course, we can write a formula or UDF, which once again selects an array of prime numbers for us. We will not engage in nonsense - this work has been done many times for us.
We can limit ourselves to a short series
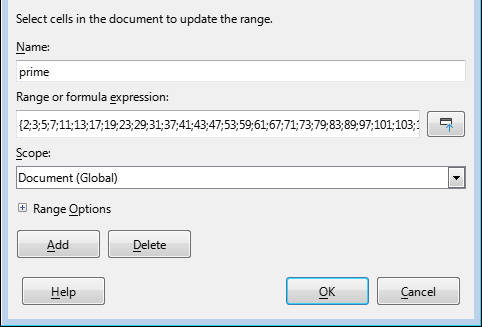
Or we can take 58 prime numbers straight from sequence A000040 in the OEIS
Or, in pursuit of perfection, we can use 1000 prime numbers
(My demo uses this set - why not?)
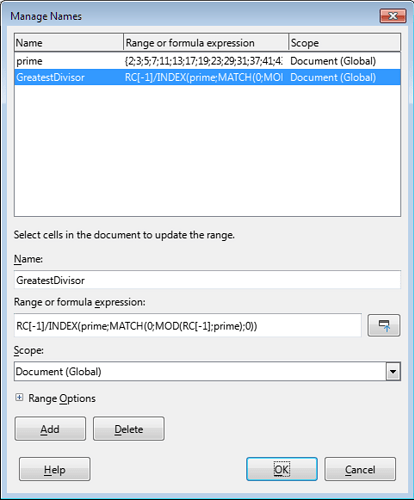
In order not to drag this array into every formula, we can write the entire sequence into a named range and call it (surprise!) “prime”
{2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59;61;67;71;73;79;83;89;97;101;103;107;109;113;127;131;137;139;149;151;157;163;167;173;179;181;191;193;197;199;211;223;227;229;233;239;241;251;257;263;269;271;277;281;283;293;307;311;313;317;331;337;347;349;353;359;367;373;379;383;389;397;401;409;419;421;431;433;439;443;449;457;461;463;467;479;487;491;499;503;509;521;523;541;547;557;563;569;571;577;587;593;599;601;607;613;617;619;631;641;643;647;653;659;661;673;677;683;691;701;709;719;727;733;739;743;751;757;761;769;773;787;797;809;811;821;823;827;829;839;853;857;859;863;877;881;883;887;907;911;919;929;937;941;947;953;967;971;977;983;991;997;1009;1013;1019;1021;1031;1033;1039;1049;1051;1061;1063;1069;1087;1091;1093;1097;1103;1109;1117;1123;1129;1151;1153;1163;1171;1181;1187;1193;1201;1213;1217;1223;1229;1231;1237;1249;1259;1277;1279;1283;1289;1291;1297;1301;1303;1307;1319;1321;1327;1361;1367;1373;1381;1399;1409;1423;1427;1429;1433;1439;1447;1451;1453;1459;1471;1481;1483;1487;1489;1493;1499;1511;1523;1531;1543;1549;1553;1559;1567;1571;1579;1583;1597;1601;1607;1609;1613;1619;1621;1627;1637;1657;1663;1667;1669;1693;1697;1699;1709;1721;1723;1733;1741;1747;1753;1759;1777;1783;1787;1789;1801;1811;1823;1831;1847;1861;1867;1871;1873;1877;1879;1889;1901;1907;1913;1931;1933;1949;1951;1973;1979;1987;1993;1997;1999;2003;2011;2017;2027;2029;2039;2053;2063;2069;2081;2083;2087;2089;2099;2111;2113;2129;2131;2137;2141;2143;2153;2161;2179;2203;2207;2213;2221;2237;2239;2243;2251;2267;2269;2273;2281;2287;2293;2297;2309;2311;2333;2339;2341;2347;2351;2357;2371;2377;2381;2383;2389;2393;2399;2411;2417;2423;2437;2441;2447;2459;2467;2473;2477;2503;2521;2531;2539;2543;2549;2551;2557;2579;2591;2593;2609;2617;2621;2633;2647;2657;2659;2663;2671;2677;2683;2687;2689;2693;2699;2707;2711;2713;2719;2729;2731;2741;2749;2753;2767;2777;2789;2791;2797;2801;2803;2819;2833;2837;2843;2851;2857;2861;2879;2887;2897;2903;2909;2917;2927;2939;2953;2957;2963;2969;2971;2999;3001;3011;3019;3023;3037;3041;3049;3061;3067;3079;3083;3089;3109;3119;3121;3137;3163;3167;3169;3181;3187;3191;3203;3209;3217;3221;3229;3251;3253;3257;3259;3271;3299;3301;3307;3313;3319;3323;3329;3331;3343;3347;3359;3361;3371;3373;3389;3391;3407;3413;3433;3449;3457;3461;3463;3467;3469;3491;3499;3511;3517;3527;3529;3533;3539;3541;3547;3557;3559;3571;3581;3583;3593;3607;3613;3617;3623;3631;3637;3643;3659;3671;3673;3677;3691;3697;3701;3709;3719;3727;3733;3739;3761;3767;3769;3779;3793;3797;3803;3821;3823;3833;3847;3851;3853;3863;3877;3881;3889;3907;3911;3917;3919;3923;3929;3931;3943;3947;3967;3989;4001;4003;4007;4013;4019;4021;4027;4049;4051;4057;4073;4079;4091;4093;4099;4111;4127;4129;4133;4139;4153;4157;4159;4177;4201;4211;4217;4219;4229;4231;4241;4243;4253;4259;4261;4271;4273;4283;4289;4297;4327;4337;4339;4349;4357;4363;4373;4391;4397;4409;4421;4423;4441;4447;4451;4457;4463;4481;4483;4493;4507;4513;4517;4519;4523;4547;4549;4561;4567;4583;4591;4597;4603;4621;4637;4639;4643;4649;4651;4657;4663;4673;4679;4691;4703;4721;4723;4729;4733;4751;4759;4783;4787;4789;4793;4799;4801;4813;4817;4831;4861;4871;4877;4889;4903;4909;4919;4931;4933;4937;4943;4951;4957;4967;4969;4973;4987;4993;4999;5003;5009;5011;5021;5023;5039;5051;5059;5077;5081;5087;5099;5101;5107;5113;5119;5147;5153;5167;5171;5179;5189;5197;5209;5227;5231;5233;5237;5261;5273;5279;5281;5297;5303;5309;5323;5333;5347;5351;5381;5387;5393;5399;5407;5413;5417;5419;5431;5437;5441;5443;5449;5471;5477;5479;5483;5501;5503;5507;5519;5521;5527;5531;5557;5563;5569;5573;5581;5591;5623;5639;5641;5647;5651;5653;5657;5659;5669;5683;5689;5693;5701;5711;5717;5737;5741;5743;5749;5779;5783;5791;5801;5807;5813;5821;5827;5839;5843;5849;5851;5857;5861;5867;5869;5879;5881;5897;5903;5923;5927;5939;5953;5981;5987;6007;6011;6029;6037;6043;6047;6053;6067;6073;6079;6089;6091;6101;6113;6121;6131;6133;6143;6151;6163;6173;6197;6199;6203;6211;6217;6221;6229;6247;6257;6263;6269;6271;6277;6287;6299;6301;6311;6317;6323;6329;6337;6343;6353;6359;6361;6367;6373;6379;6389;6397;6421;6427;6449;6451;6469;6473;6481;6491;6521;6529;6547;6551;6553;6563;6569;6571;6577;6581;6599;6607;6619;6637;6653;6659;6661;6673;6679;6689;6691;6701;6703;6709;6719;6733;6737;6761;6763;6779;6781;6791;6793;6803;6823;6827;6829;6833;6841;6857;6863;6869;6871;6883;6899;6907;6911;6917;6947;6949;6959;6961;6967;6971;6977;6983;6991;6997;7001;7013;7019;7027;7039;7043;7057;7069;7079;7103;7109;7121;7127;7129;7151;7159;7177;7187;7193;7207;7211;7213;7219;7229;7237;7243;7247;7253;7283;7297;7307;7309;7321;7331;7333;7349;7351;7369;7393;7411;7417;7433;7451;7457;7459;7477;7481;7487;7489;7499;7507;7517;7523;7529;7537;7541;7547;7549;7559;7561;7573;7577;7583;7589;7591;7603;7607;7621;7639;7643;7649;7669;7673;7681;7687;7691;7699;7703;7717;7723;7727;7741;7753;7757;7759;7789;7793;7817;7823;7829;7841;7853;7867;7873;7877;7879;7883;7901;7907;7919;1}
One trick needs to be mentioned: the sequence of prime numbers ends with 1 - we put 1 at the very end of the array. This will allow the formula to always return 0 as a result of calculating the remainder of the division - no need additional error checking.
Now the formula will do all the work
=A1/INDEX(prime;MATCH(0;MOD(A1;prime);0))
or in RC notation
=RC[-1]/INDEX(prime;MATCH(0;MOD(RC[-1];prime);0))
What an awkward entry! @andy-andyo , why are you using this?
Moreover, we have every right to place this formula in a named range and call it, for example, GreatestDivisor
So, the largest prime number that participates in the checks is 7919. This means that numbers up to and including 62710561 will be processed without errors. Even larger numbers will also be processed and most often without errors, but I would not risk it. For what? Sixty-two million, seven hundred and ten thousand, five hundred and sixty-one is really a lot.
Yes, this formula does not fulfill this requirement:
As for me, I don’t see much difference between 1 and -1. At worst, we can always display 1 as -1 and even color it red. Here’s how it all works - GD.ods (32.1 KB)
Hi
Thank you all for all the suggestions to resolve my query, or at least partially resolve it and get steps closer to making my spreadsheet work. As a complete amateur mathematician it will take me some time to digest the solutions and see if they work in my spreadsheet, I’m bit slow these days so please allow me some time to try out the suggestions.
The reason I’m doing this is to try and flag up/list a set of numbers which my spreadsheet produces and leave others. The list of initial (starting) numbers is essentially random, there being composites and primes and all of them whole numbers. Its the composites I’m interested in. This is why I’m trying to identify the greatest-divisor-numbers, as I wish to end up with a list that is composed of only numbers with 2 denominators (factors). This list will originate from the spreadsheet results so far. I’m not trying to develop a list of all the composites. That would be easy I think. I have been looking at all things prime (here and there, on and off) for about 4 years now (not just for this) because they are an opposing set of numbers.
My problem is I do not know enough about the spreadsheet itself; I tried a few formulae that needed to be entered as range-formula but could not get them to work. Whereas I’m sure this sort of thing is easy for you.
About the limit - there is none.
I know that at some point the numbers will get too large for processing, and it will take the computer so long I could be dead. However the principal is the important thing as the number list I may get (as large as is manageable, -say a few million) will input into another (spreadsheet or whole set of columns in this one) to produce results there.
I will do my best to try copying the formulae suggested tomorrow as have other duties today. I really appreciate your input.
Thanks
Andy
Hi- this formula```
=IFS(RC[-1]<4;-1;ISEVEN(RC[-1]);RC[-1]/2;1;MAX(IF(MOD(RC[-1];(ROW(R1C:INDEX(C;SQRT(RC[-1]/4)))*2)+1)=0;RC[-1]/(ROW(R1C:INDEX(C;SQRT(RC[-1]/4)))*2+1); -1)))
Produces a result
2 -1
3 -1
4 2
5 -1
6 3
7 -1
8 4
9 3
10 5
11 -1
12 6
13 -1
14 7
15 5
16 8
17 -1
18 9
19 -1
20 10
21 7
22 11
23 -1
24 12
25 -1
26 13
27 9
28 14
29 -1
30 15
31 -1
32 16
33 11
34 17
35 -1
36 18
37 -1
38 19
39 13
40 20
41 -1
42 21
43 -1
44 22
45 15
46 23
47 -1
48 24
49 -1
50 25
51 17
52 26
53 -1
54 27
55 -1
56 28
57 19
58 29
59 -1
60 30
61 -1
62 31
63 21
64 32
65 -1
66 33
67 -1
68 34
69 23
70 35
71 -1
72 36
73 -1
74 37
75 25
76 38
77 -1
This formula is identifying primes without any problems except that it sees 25 as indicative of a prime i.e =-1. Then going further it identifies 35 the same, and so
35, 49, 55, 65, 77, then 91, and so on (This is no good). These numbers should be showing at least, 5, 7, 7, 11, 13, 11, 13... My mistake is that I would prefer the resultant to be the greatest Factor of the number being considered. But it should not show a factorisable/denomitor-able number as a prime. Andy just had to test - I'm now gone for day, - sorry.Calc has only one number type. That’s ‘Double’ and is iimplemented as IEEE 754 Double. It uses 8 bytes (64 bits) in RAM, but is optimized for “floating-point” operations and has only an effective mantissa of 52 bits. The content of a respective varible is surely NOT representing a whole number in many cases. If it can be supposd to represent one in different cases is a ticklish question. The best test for “may be a positive integer” in Calc I can think of is
(thing > 0) AND (((thing + 1) - thing)=1), but it also can’t tell if not there was rounding or whatever during calculations. Basic doesn’t help with this because its integer types only allow for LongInt with a 4-byte-resolution, and the largest positive integer it can hold is therefore 2^31-1 (2147483647). The largest integer representable in the above mentioned sense in Calc is 9007199254740991.
For questions of number theory (of which divisibility is a typical one), such numbers are tiny sub-dwarfs. Neither any spreadshet software nor any programming language for “general purposes” has means for the field. Any software made for the support of mathematical work has. The free and open Maxima, e.g, returns the factorization below “in no time” (and a number of 20 decimal digits would also not be a problem). To get it in Calc with the help of Basic you might need a few days of programming, a lot of run-time, and the faith to believe in the result for which there wouldn’t be independent checks.
factor(9007199254740991);
6361*69431*20394401
Largest factor in your sense: 1416003655831. Howto check with Calc or Basic? No chance. Use a sheet of paper an a pencil.
You had missed the requirement to use array formula.
Function Wizard indicates that there is an error.
=IFS(RC[-1]<4,-1,ISEVEN(RC[-1]),RC[-1]/2,1,MAX(IF(MOD(RC[-1],(ROW(R1C:INDEX(C,SQRT(RC[-1]/4)))*2)+1)=0,RC[-1]/(ROW(R1C:INDEX(C,SQRT(RC[-1]/4)))*2+1), -1)))
This formula is identifying primes without any problems except that it sees 25 as indicative of a prime i.e. =-1. Then going further it identifies 35 the same, followed by 49, 55, 65, 77, then 91…, and so on.
Ideally these numbers should be showing at least, 5, 7, 7, 11, 13, 11, 13… The largest divisor or possibly the greatest factor because they are composites.
The error shown in function wizard is for the part
(ROW(R1C:INDEX(C,SQRT(RC[-1] at INDEX(C , which is C=#VALUE! {;;;;;-1;-1;-1;-2;…
Or is it actually an error at all? Is this a way of stopping LO Calc from flagging up the error?
Also the ROW reference is to the following row. Is this correct? My original statement was for ‘one greatest divisor number per row’ - referencing the (list) number in that row. Ideally I do not want referencing in the formula to previous or later rows. One of my reasons for this is that Calc is not reliable to return the spreadsheet to its original state if a Sort is carried out; this is due to formula results getting scramble in the Sort. (So the Sort has to be carried out on a Values only basis, with formulas cleared off the sheet.)
While I have carried out testing on a list which is the Number Line, this will not be the case in usage. The list of numbers will be random and values not in order of size.
So having thrown as many spanners into the works as I can -
Is there anyway of stopping the numbers above from being listed as -1. the numbers ending in 5 are simple as they can be seived out, but not the others.
I’m intrigued by these obviously composite numbers being grouped with primes when they should not be there at all.
Apologies for the Encyclopaedia I am writing-
Sunday regards
Andy
Still testing -
Hi Mike
Sorry for being stupid. I am trying to copy and paste the formula in to the cell, and have tried directly into the formula bar- but it does not work. I do not know how to copy an array {} formula. I also noticed that I could not copy it in to additional cells in the sheet you sent me by dragging down.
This is something the whole World knows how to do except me I think.
Thanks for the .ODS by the way.
Andy
 No, what you see is not that straightforward.
No, what you see is not that straightforward.
- To enter an array formula into a cell, you need to press Ctrl+Shift+Enter after you finished typing the formula.
- If you already have a formula in the cell, and want to turn it into an array formula, you must do an edit in the formula first (to mark it changed, and force formula compiler to re-compile it) - e.g., as simple as adding a space in the end, and then remove the space using Backspace key.
- Alternatively, you can create array formulas using
Formula Wizard- the wizard has respective checkbox in the bottom left corner. But that checkbox can’t be used to make an array formula not array. - Every array formula has a region; and when you have created an array formula region, you only can edit the formula when you have selected the whole region. Since it’s not always obvious where this region is, you need to select one cell in that region first, then press Ctrl+/ to select the whole region.
- You can drag the corner in the usual way, e.g. to increase the array formula region.
- But in this specific case, you must not change the one-cell array formula into many-cell array formula, by dragging the corner. Every cell with such a formula must have an own array range. To do this, you can simply copy the cell with existing array formula, then select the area where you want to copy it, and then paste.
HTH.
Copy the entire cell instead of the formula.
Thanks Mike & Villeroy
I will try that all right
Andy