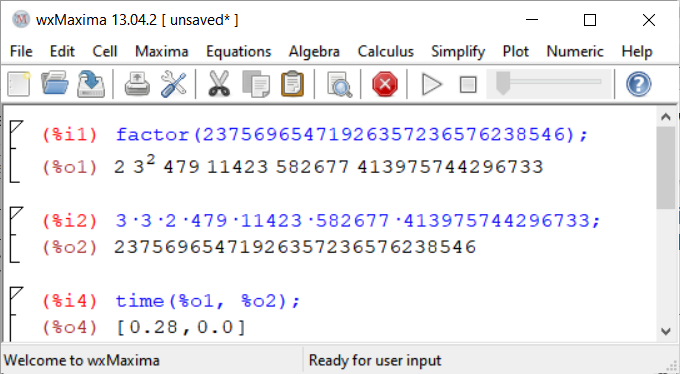
Okay, let’s try this approach.
@Lupp, thanks for the tip - indeed, working with prime numbers is much more convenient than iterating over all the row numbers in a column.
So, we use Lupp’s idea - we look at the remainder of dividing a given number by each “known” prime number. As soon as we meet the remainder of the division equal to 0, we divide the original number by the found prime number and get the largest divisor.
Where to get prime numbers? Of course, we can write a formula or UDF, which once again selects an array of prime numbers for us. We will not engage in nonsense - this work has been done many times for us.
We can limit ourselves to a short series
Or we can take 58 prime numbers straight from sequence A000040 in the OEIS
Or, in pursuit of perfection, we can use 1000 prime numbers
(My demo uses this set - why not?)
In order not to drag this array into every formula, we can write the entire sequence into a named range and call it (surprise!) “prime”
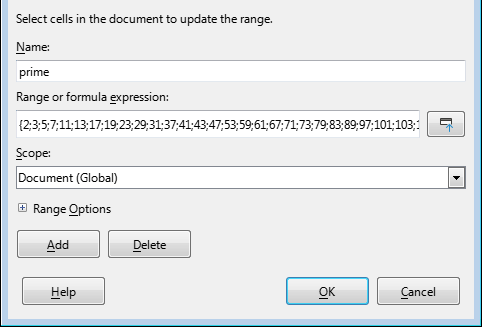
{2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59;61;67;71;73;79;83;89;97;101;103;107;109;113;127;131;137;139;149;151;157;163;167;173;179;181;191;193;197;199;211;223;227;229;233;239;241;251;257;263;269;271;277;281;283;293;307;311;313;317;331;337;347;349;353;359;367;373;379;383;389;397;401;409;419;421;431;433;439;443;449;457;461;463;467;479;487;491;499;503;509;521;523;541;547;557;563;569;571;577;587;593;599;601;607;613;617;619;631;641;643;647;653;659;661;673;677;683;691;701;709;719;727;733;739;743;751;757;761;769;773;787;797;809;811;821;823;827;829;839;853;857;859;863;877;881;883;887;907;911;919;929;937;941;947;953;967;971;977;983;991;997;1009;1013;1019;1021;1031;1033;1039;1049;1051;1061;1063;1069;1087;1091;1093;1097;1103;1109;1117;1123;1129;1151;1153;1163;1171;1181;1187;1193;1201;1213;1217;1223;1229;1231;1237;1249;1259;1277;1279;1283;1289;1291;1297;1301;1303;1307;1319;1321;1327;1361;1367;1373;1381;1399;1409;1423;1427;1429;1433;1439;1447;1451;1453;1459;1471;1481;1483;1487;1489;1493;1499;1511;1523;1531;1543;1549;1553;1559;1567;1571;1579;1583;1597;1601;1607;1609;1613;1619;1621;1627;1637;1657;1663;1667;1669;1693;1697;1699;1709;1721;1723;1733;1741;1747;1753;1759;1777;1783;1787;1789;1801;1811;1823;1831;1847;1861;1867;1871;1873;1877;1879;1889;1901;1907;1913;1931;1933;1949;1951;1973;1979;1987;1993;1997;1999;2003;2011;2017;2027;2029;2039;2053;2063;2069;2081;2083;2087;2089;2099;2111;2113;2129;2131;2137;2141;2143;2153;2161;2179;2203;2207;2213;2221;2237;2239;2243;2251;2267;2269;2273;2281;2287;2293;2297;2309;2311;2333;2339;2341;2347;2351;2357;2371;2377;2381;2383;2389;2393;2399;2411;2417;2423;2437;2441;2447;2459;2467;2473;2477;2503;2521;2531;2539;2543;2549;2551;2557;2579;2591;2593;2609;2617;2621;2633;2647;2657;2659;2663;2671;2677;2683;2687;2689;2693;2699;2707;2711;2713;2719;2729;2731;2741;2749;2753;2767;2777;2789;2791;2797;2801;2803;2819;2833;2837;2843;2851;2857;2861;2879;2887;2897;2903;2909;2917;2927;2939;2953;2957;2963;2969;2971;2999;3001;3011;3019;3023;3037;3041;3049;3061;3067;3079;3083;3089;3109;3119;3121;3137;3163;3167;3169;3181;3187;3191;3203;3209;3217;3221;3229;3251;3253;3257;3259;3271;3299;3301;3307;3313;3319;3323;3329;3331;3343;3347;3359;3361;3371;3373;3389;3391;3407;3413;3433;3449;3457;3461;3463;3467;3469;3491;3499;3511;3517;3527;3529;3533;3539;3541;3547;3557;3559;3571;3581;3583;3593;3607;3613;3617;3623;3631;3637;3643;3659;3671;3673;3677;3691;3697;3701;3709;3719;3727;3733;3739;3761;3767;3769;3779;3793;3797;3803;3821;3823;3833;3847;3851;3853;3863;3877;3881;3889;3907;3911;3917;3919;3923;3929;3931;3943;3947;3967;3989;4001;4003;4007;4013;4019;4021;4027;4049;4051;4057;4073;4079;4091;4093;4099;4111;4127;4129;4133;4139;4153;4157;4159;4177;4201;4211;4217;4219;4229;4231;4241;4243;4253;4259;4261;4271;4273;4283;4289;4297;4327;4337;4339;4349;4357;4363;4373;4391;4397;4409;4421;4423;4441;4447;4451;4457;4463;4481;4483;4493;4507;4513;4517;4519;4523;4547;4549;4561;4567;4583;4591;4597;4603;4621;4637;4639;4643;4649;4651;4657;4663;4673;4679;4691;4703;4721;4723;4729;4733;4751;4759;4783;4787;4789;4793;4799;4801;4813;4817;4831;4861;4871;4877;4889;4903;4909;4919;4931;4933;4937;4943;4951;4957;4967;4969;4973;4987;4993;4999;5003;5009;5011;5021;5023;5039;5051;5059;5077;5081;5087;5099;5101;5107;5113;5119;5147;5153;5167;5171;5179;5189;5197;5209;5227;5231;5233;5237;5261;5273;5279;5281;5297;5303;5309;5323;5333;5347;5351;5381;5387;5393;5399;5407;5413;5417;5419;5431;5437;5441;5443;5449;5471;5477;5479;5483;5501;5503;5507;5519;5521;5527;5531;5557;5563;5569;5573;5581;5591;5623;5639;5641;5647;5651;5653;5657;5659;5669;5683;5689;5693;5701;5711;5717;5737;5741;5743;5749;5779;5783;5791;5801;5807;5813;5821;5827;5839;5843;5849;5851;5857;5861;5867;5869;5879;5881;5897;5903;5923;5927;5939;5953;5981;5987;6007;6011;6029;6037;6043;6047;6053;6067;6073;6079;6089;6091;6101;6113;6121;6131;6133;6143;6151;6163;6173;6197;6199;6203;6211;6217;6221;6229;6247;6257;6263;6269;6271;6277;6287;6299;6301;6311;6317;6323;6329;6337;6343;6353;6359;6361;6367;6373;6379;6389;6397;6421;6427;6449;6451;6469;6473;6481;6491;6521;6529;6547;6551;6553;6563;6569;6571;6577;6581;6599;6607;6619;6637;6653;6659;6661;6673;6679;6689;6691;6701;6703;6709;6719;6733;6737;6761;6763;6779;6781;6791;6793;6803;6823;6827;6829;6833;6841;6857;6863;6869;6871;6883;6899;6907;6911;6917;6947;6949;6959;6961;6967;6971;6977;6983;6991;6997;7001;7013;7019;7027;7039;7043;7057;7069;7079;7103;7109;7121;7127;7129;7151;7159;7177;7187;7193;7207;7211;7213;7219;7229;7237;7243;7247;7253;7283;7297;7307;7309;7321;7331;7333;7349;7351;7369;7393;7411;7417;7433;7451;7457;7459;7477;7481;7487;7489;7499;7507;7517;7523;7529;7537;7541;7547;7549;7559;7561;7573;7577;7583;7589;7591;7603;7607;7621;7639;7643;7649;7669;7673;7681;7687;7691;7699;7703;7717;7723;7727;7741;7753;7757;7759;7789;7793;7817;7823;7829;7841;7853;7867;7873;7877;7879;7883;7901;7907;7919;1}
One trick needs to be mentioned: the sequence of prime numbers ends with 1 - we put 1 at the very end of the array. This will allow the formula to always return 0 as a result of calculating the remainder of the division - no need additional error checking.
Now the formula will do all the work
=A1/INDEX(prime;MATCH(0;MOD(A1;prime);0))
or in RC notation
=RC[-1]/INDEX(prime;MATCH(0;MOD(RC[-1];prime);0))
What an awkward entry! @andy-andyo , why are you using this?
Moreover, we have every right to place this formula in a named range and call it, for example, GreatestDivisor
So, the largest prime number that participates in the checks is 7919. This means that numbers up to and including 62710561 will be processed without errors. Even larger numbers will also be processed and most often without errors, but I would not risk it. For what? Sixty-two million, seven hundred and ten thousand, five hundred and sixty-one is really a lot.
Yes, this formula does not fulfill this requirement:
As for me, I don’t see much difference between 1 and -1. At worst, we can always display 1 as -1 and even color it red. Here’s how it all works - GD.ods (32.1 KB)

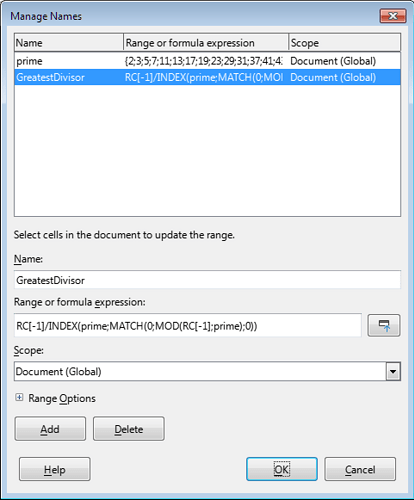
 No, what you see is not that straightforward.
No, what you see is not that straightforward.