LINEST
https://forum.openoffice.org/en/forum/download/file.php?id=20612
That is not really what I was looking for. It is also not obvious from the example how the array function is entered; when I try to edit it, a box pops up that says “You cannot change only part of an array”. Are there instructions for using this method in the Calc Help pages? Or somewhere.
In Google Sheets, the function =ArrayFormula(LINEST(B2:B12,A2:A12^{1,2})) returns an array of coefficients for a second order polynomial directly without the user having to create the column of x² values. Or columns of x³ etc for higher order polynomials.
From the Help:
LINEST returns a table (array) of statistics as below and must be entered as an array formula (for example by using Ctrl + Shift + Return rather than just Return).
The link also has information on editing, copying and adjusting array formulae.
Thanks for the link, but I must be misunderstanding something. The description of LINEST at the link says “Returns a table of statistics for a straight line that best fits a data set” but I am asking about polynomials (curves) that fit data where the relationship is not linear.
Thanks for your answer. I know this can be done by graphing the data and fitting a trendline, displaying the trendline equation and then copying the trendline coefficients. I do this by taking a screenshot and running an OCR to get the coefficients that I can paste into the spreadsheet. But it’s not an elegant way of getting the coefficients. To show the coefficients, the graph is following an algorithm in the background using LINEST to extract them from the data. It would be nice if the same algorithm was implemented as a spreadsheet function.
Did you try LINEST() meanwhile?
Hi Lupp, yes, I did try LINEST() and it works, of course. Now I have tried it, I will probably use it again, but having to create the column of x² values for a second order polynomial fit makes a mess of my tidy spreadsheet.
I found the explanation of LINEST in the Help section pretty well impossible to understand, and it doesn’t seem to cover using LINEST for polynomials at all. Perhaps we could work on a better version?
An additional helper sheet that can be shown or hidden on demand is very cheap. Anyway your design should surely be correct and efficient in the first place, and a “neat and tidy” sheet for a printout is cheap again, and can draw any data from the efficient working sheets as needed.
If you aren’t interested in the diagram itself, but only in the coefficients for a polynomial approximation, it’s surely not recommendable to use a diagram as a helper only, and even to use OCR then.
Out of interset I tried to find a chart property for the trendline formula, but didn’t succeed.
In a kind of playful mood, I then used an existing self-made template with custom code by @Lupp, added a function collectColumns() to it, and made a “neat and tidy” spreadsheet doing the trick solely based on the X- and Y-columns needed anyway to get the coefficients, but without showing the used helper columns to find the coefficients for the polynomial approximation (degree 5 in the example).
As already told the solution needs to run user code. If you are interested nevertheless I will attach the example to another comment.
that’s Teasing ! 
I am not a native English speaker and rarely sure about the meaning of colloquial expressions. Now I’ll just attach the example I mentioned and everyone can decide if they want to study it.
Please understand that a polynomial approximation of fifth order will rarely be appropriate. The example is very special insofar.
disask114304relatedPolyApproxByLinestUsingBsmY.ods (62.6 KB)
The “LIN” in the name LINEST not mean that the result always will be a straight line. It shows the type of the equation and the calculated coefficients.
It is not a spreadsheet-related information. It is a matematics-related information.
This is well known.
What I said was that there is no explanation in the help file for using the LINEST function to find the coefficients of polynomials, or other functions of x such as logarithms or powers for example. If there is an explanation, then I either couldn’t find it or I didn’t understand it.
There is an example table at the end of this article with two columns of (x1), (x2) values. You can use more than two x columns, and you can use these columns (of the x values) as indepentent variables, or you can use them as (x1)^1, (x1)^2, (x1)^3 calculated from same x values as “one variable in a polinomial form”… Of course you can use other exponents too.
https://wiki.documentfoundation.org/Documentation/Calc_Functions/LINEST
I wouldn’t claim that I have read everything the help contains about LINEST(), and I did not study the en.wikipedia article that was linked. However I also feel that the help is misleading when telling
Summary:
Calculates the straight line that best fits a supplied data set and optionally returns detailed statistics on the regression
but nowhere mentioning polynomials.
If the couple of given vectors happens to be made from successive powers of x this gives the coefficients for the (a) “best fitting polynomial”.
This is surely difficult to understand for users not very familiar with mathematics, and the detailed definition and explanation of LINEST() in the respective odf (OASIS) document under subchapter 6.18.41 fills more than 3 pages.
Harmonic, exponential or logarithmic approximations are not covered by linest. See LOGEST() if interested.
In more special cases a nonlinear solver may find a satisfying fit.
FWIW:
see the Help topic Trend Lines (polynomial trend line, Calculate Parameters in Calc – the polynomial regression equation).
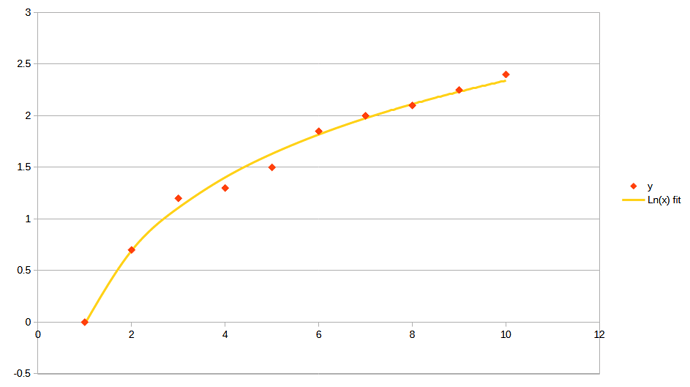
LINEST does cover Harmonic, exponential and logarithmic approximations. LINEST doesn’t inherently “know” what problem it’s solving, it allows you to provide any set of independent variables that you think might fit your data. For example, if you think your data might fit a logarithmic model, create a column of ln(x) and use that as the x input data. LINEST will return the coefficients a and b of y = a ln(x) + b. The graphic shows an example of a ln(x) fit by LINEST.