Bonjour
Dans une feuille, j’ai 4 colonnes A,B,C et D. Dans D j’ai une formule de vérification : =A-B-C dont le résultat doit toujours être à 0 (pour détecter d’éventuelles erreurs de saisie).
Plus d’une centaine de lignes affichent bien 0, mais je viens de trouver une ligne avec la valeur “-0”, ce qui m’a intrigué.
Après recherches et vérifications, je me rends compte que la valeur stockée est de l’ordre de -7,9E-15
J’ai fait des essais avec différentes valeurs : parfois, on trouve 0, parfois une valeur résiduelle du même ordre de grandeur, généralement négative, mais parfois aussi positive.
Est-ce que quelqu’un a déjà observé ce problème et peut m’éclairer.
Dans mon cas, ce n’est pas vraiment gênant, mais cela m’a permis d’écrire une formule qui, alors que le résultat attendu est 0 peut renvoyer des valeurs fantaisistes.
Exemple :
(122,34-120,55-1,79)*1E+20=0 (OK)
(122,35-120,56-1,79)*1E+20=-799 360,58 (Bizarre !)
J’ai fait les calculs en remplaçant la formule =A-B-C par =A-(B+C), mathématiquement équivalente. Le problème est moins fréquent, mais existe toujours pour certaines valeurs.
J’ai une feuille de calcul avec tous ces essais, mais je ne sais pas si c’est possible de la joindre à ce message.
Merci à qui pourra m’apporter des explications.
Jean-Marie
Un tableur, à cause du stockage des nombres en virgule flottante, ne permet une précision que de 15 chiffres. Il n’est donc pas possible de travailler avec de si grand nombres.
Bonjour,
test intéressant à faire.
Dans un moteur de recherche (Startpage pour moi), taper successivement les deux versions. On obtient zéro dans les deux cas, les programmes utilisés par les serveurs n’ont pas les mêmes limites qu’un tableur.
(122,35-120,56-1,79)*1E+020 = 0
(122,34-120,55-1,79)*1E+020 = 0
Dans un contexte professionnel, où j’utilisais Excel, j’avais dû mettre en place des tests de comparaison pour forcer à zéro toute valeur inférieure à un seuil défini.
Exception peu banale à l’époque, dans les années 90, le tableur de Framework (Ashton-Tate) poussait la précision des calculs à 64 décimales.
Bonjour et merci pour la réponse.
En fait, je n’ai donné la multiplication par un grand nombre que pour illustrer le problème. Je sais que la représentation des nombres en virgule flottante limite la précision, mais il reste des incohérences.
Je n’ai entré que des données avec 2 décimales et ne devrais donc pas être perturbé par un écart de l’ordre de 10^-15.
Par ailleurs, aucune indication de la limite de précision n’apparaît.
J’ai complété mes investigations :
si je calcule l’inverse du résultat (attendu à 0), j’obtiens soit, comme attendu, une erreur #DIV/0!, soit un très grand nombre.
si je fais compare le calcul : A-B-C à A-(B+C), je trouve un résultat inférieur, égal ou supérieur, suivant les cas. Ça n’inspira pas confiance !
Ce qui me rassure pour Libre Office, c’est que MS Excel ne fait pas mieux 
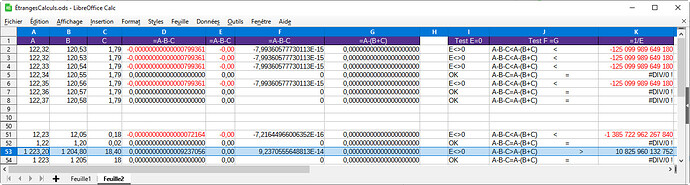
Voici une copie partielle de mes essais pour que cela soit plus explicite.
Jean-Marie
Bonjour,
Ça n’inspira pas confiance !
Je pense qu’il faut s’approprier l’outil avec ses limites, son domaine d’usage “raisonnable”.
Dans les contextes particulièrement exigeants, l’usage d’outils bureautiques généralistes n’est pas le mieux adapté.
On aura je pense des résultats plus fiables avec des outils spécialisés, conçus pour le calcul scientifique, les statistiques.
aucune indication de la limite de précision n’apparaît
Pas facile de trouver l’info en effet. Le wiki renvoie à IEEE 754 - Wikipedia
Il serait intéressant d’étudier la fonction ‘soustraire.brut’, ‘RAWSUBTRACT’ en anglais. Je n’ai pas les compétences pour en parler.
Voir Documentation/Calc Functions/RAWSUBTRACT - The Document Foundation Wiki
Bonjour, voir aussi peut être la page d’aide à ce sujet :
https://help.libreoffice.org/latest/fr/text/scalc/01/calculation_accuracy.html?DbPAR=CALC
Bonjour
Vos réponses et les informations fournies m’ont permis de mieux comprendre.
Je n’avais pas trouvé la page d’aide qui résume bien la question. Effectivement, le sujet est compliquée et je comprends le choix qui a été fait de ne pas chercher à traiter tous les cas marginaux.
Mais ça fait quand même bizarre quand l’utilisation élémentaire d’une fonction de test (SI) vous annonce sans sourciller que, par exemple, 12,23-12,05-0,18 est plus petit que 12,23 -(12,05+0,18)…
Merci de votre aide.
Jean-Marie
Bonjour,
on obtient des résultats différents selon qu’on utilise des opérateurs ou des fonctions. Cela incite en effet à la prudence et à des vérifications croisées avant de “faire confiance”, voire de prendre des décisions critiques sur la base de tels calculs.
Ci-joint un document Calc avec les tests effectués.
precision_calcul.ods (12,8 Ko)