Umwandeln eines binären Codes in bit-weises Invertieren

[koyotak]

Eine digitale Zahl im binären Format will ich umwandeln, so dass bit-für-bit invertiert wird, d.h.: „0“ → „1“ ODER „1“ → „0“.
In Zelle [A1] gebe ich die n×4-bit-Zahl ein, in [B1] die n-Anzahl der 4er-Blöcke, also 4-bit, 8-bit (= 1-Byte), 16-bit (= 2-Byte), 32-bit (= 4-Byte), 64-bit (= 8-Byte). In Zelle [A2] will ich das investierte Ergebnis sehen.
Die Eingabe [A1] im TEXT-Format ist einfach, im ZAHL-Format bedingt die Angabe der Anzahl fixer Stellen (4, 8, 16, 32, 64), was ohnehin die Auswahl mittels Daten-Gültigkeit [B1] bedingt.

Beispiele:
a) 0000 0110 [A1] nach 1111 1001 [A2] @ 8-bit [B1], die hier „sichtbar“ aufgefüllten vorangestellten Nullen sind inbegriffen;
b) 1110 1000 nach 1111 1111 0001 0111 @ 16-bit, die „unsichtbaren“ 8 MSBs (most significant bits), die ja mit Nullen aufgefüllt werden (1110 1000 → 0000 0000 1110 1000) stets nach Einsen wandeln.

Umgekehrtes Invertieren ist einfach:
Solange ich jede CALC-Zelle jeweils nur mit 1-bit (0 oder 1) fülle, ist die Sache einfach: 16 Zellen [A2]…[P2] belegt mit =NiCHT(A1) bis =NiCHT(P1) @ 2-Byte = 16-bit. Bei mehr Bytes wird die Sache „unappetitlich“!
Die invertierte binäre Zahl im Text-Format erhalte ich mit: =VERBiNDEN("";0;A2:P2). Im Text-Format werden – wie gewünscht – keine vorangestellten Nullen unterdrückt, wie bei Zahlen üblicherweise.

Nun zur eigentlichen Aufgabe: Der umgekehrte Weg, wie in den 2 Beispielen mit nur 3 CALC-Zellen, gelingt mir nicht!

[RobertG]

Ich hätte das viel anders gelöst, aber vielleicht hast Du ja nicht tatsächlich binäre Werte:
A1 ist eine Zahl,
B1 =DEZINBIN(A1;8)
C1 =DEZINBIN((255-A1);8)
B1 und C1 sehen genau gegensätzlich aus.

[karolus]

Hallo

a = 411
e = a.bit_length()
c = 2**e-a-1

print(f"{(line:='#'*35)}\n# {a = }\tbin {a = :0{e}b} #"
      f"\n# {c = }\tbin {c = :0{e}b} #\n{line}")
###################################
# a = 411       bin a = 110011011 #
# c = 100       bin c = 001100100 #
###################################

[koyotak]

Mein plug-in lässt nur maximal 10-stellige binäre Zahlen zu: von –512(dez)…0…+511(dez). Somit gibt beispielsweise =DEZiNBiN(1024) den Fehler:502 aus. Gleiches bei HEX- und OKT-Zahlen.

---

Uneingeschränkt ist nur die Umwandlung =DEZiMAL(n;2) von binär nach dezimal.

[koyotak]

@karolus,
teste mit anderen Zahlen als „411“!?

[karolus]

@koyotak

mit anderen Zahlen

a = 998877665544332211
…

###################################
# a = 998877665544332211        bin a = 110111011100101110011111000111001100110101110110001110110011 #
# c = 154043839062514764        bin c = 001000100011010001100000111000110011001010001001110001001100 #
###################################

zufrieden?

[koyotak]

@karolus
schade, leider nicht wie gewünscht, denn eingehender betrachtet sollen
###################################
a = 411 bin a = 0001 1001 1011
c = 3684 bin c = 1110 0110 0100
###################################
ergeben, wenn 3× 4er-Blöcke (gleich wie 4× 3er-Blöcke) gewählt sind;
oder
###################################
a = 411 bin a = 0000 0001 1001 1011
c = 65124 bin c = 1111 1110 0110 0100
###################################
, wenn 4× 4er-Blöcke gewählt sind. Bei gewählten 5× 3er- entfällt das MSB und c wird zu 32356.
Ich vermute, dass mathematische Algorithmen ausscheiden.

[karolus]

@koyotak

Ich vermute, dass mathematische Algorithmen ausscheiden.

Deine »Vermutung« ist falsch…
e = a.bit_length() berechnet lediglich die mindestens benötigte Länge.
das darfst du gerne durch deine willkürlich festgelegten Blocklängen von 3x4 = 12, 4x4 = 16 , oder auch 3x5=15 ersetzen. ⇒

a = 411 
e =  15 # 
c = 2**e-a-1

print(f"{(line:='#'*35)}\n# {a = }\tbin {a = :0{e}b} #"
      f"\n# {c = }\tbin {c = :0{e}b} #\n{line}")

###################################
# a = 411       bin a = 000000110011011 #
# c = 32356     bin c = 111111001100100 #
###################################

[koyotak]

Alternative ist erstaunlich einfach:

1. Schritt: A2=REGAUS(A1;“0”;“x”;“g”) wandelt jede „0“ in „x“ um, um den nächsten Schritt möglich zu machen;
2. Schritt: A3=REGAUS(A2;“1”;“0”;“g”) wandelt jede „1“ in „0“ um, denn die originalen „0“ sind nicht mehr vorhanden;
3. Schritt: A4=REGAUS(A3;“x”;“1”;“g”) gibt die investierte binäre Zahl aus.

[karolus]

Noch erstaunlicher:

=WECHSELN(WECHSELN(WECHSELN(A1;0;"@");1;0);"@";1)

[karolus]

@koyotak

investierte

inverierte?

[koyotak]

@karolus : inverierte?!
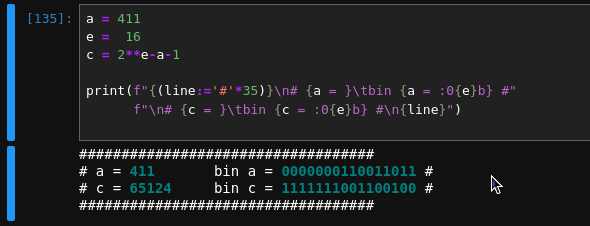
Der iQ von Goebbels Ki tendiert gegen 1 und korrigiert nach Absurdem! Wie GOOGLEs nach Goebels. Solche Schreibfehler hatte ich nicht Mal in der 1. Klasse! 🫣:cowboy_hat_face:

[karolus]

@koyotak

Solche Schreibfehler hatte ich nicht Mal in der 1. Klasse

ach … ist das so?

@koyotak

Schritt: A4=REGAUS(A3;“x”;“1”;“g”) gibt die investierte binäre Zahl aus.

[koyotak]

0_LO-CALC_ZAHL 24-bit_binäre invertieren und in dezimale umwandeln_031840.ods (18.2 KB)
… für jene Digital-Nerds, die sich mit Tab-Calculs „rumschlagen“.