How to plot a polynomial curve?

[marianoju]

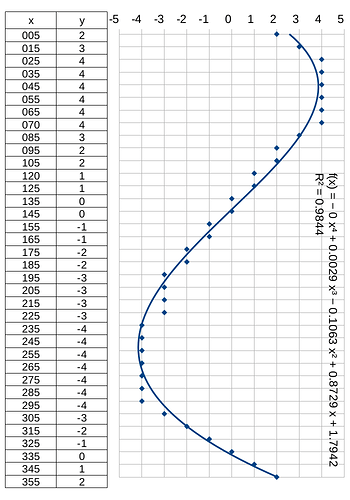
I have used Calc to perform a polynomial regression on a two-dimensional dataset (x,y) by

1. charting the two-dimensional dataset as a scatterplot (Chart Type: Line, Points Only),
2. fitting a polynomial curve with 4 degrees (Insert Trend Line), and
3. displaying the coefficient of determination of a linear regression and the equation of the polynomial curve (Insert R² and and Trend Line Equation).

The coefficient of determination is very good (0.984) and the trend line fits the data.

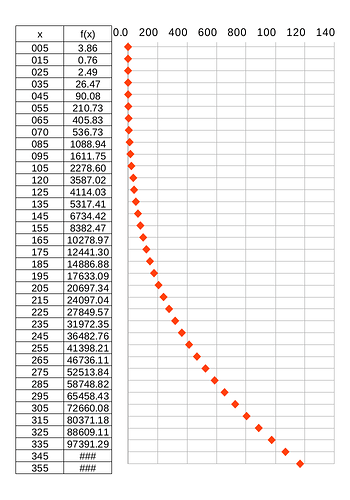
I have then applied the equation of the polynomial curve to calculate values of y given x, but the results do not fit the data, the error/divergency increases with x.

The “Trend Line Equation” is:
f(x) = - 0 x^4 + 0.0029 x^3 - 0.1063 x^2 + 0.8729 x + 1.7942

I have applied the following function:
=-(0A2^4)+(0.0029A2^3)-(0.1063A2^2)+(0.8729A2)+1.7942

My questions are

1. Can the coefficient of determination of a linear regression (R²) provide valid information about the fit of a polynomial curve?
2. What is/are the alternative/s?
3. How do I calculate y given x using the “Trend Line Equation”?

EDIT

• 190523_scatter_plot_4_degrees.ods
• 190523_scatter_plot_4_degrees.png
• 190524_polynomial curve.ods
• 190524_polynomial curve_2.png

[Lupp]

Always (except for very rare cases) attach or make available “the real thing”, here the .ods.
I will see to get enough “karma” for you to be able to attach directly to your question (by editing it).
Did you already try a polynomial approximation using LINEST()? (Do you know how?)
355^4 is about 1.6*10^10. The predefined format of the topmost coefficient surely suppresses significant digits. Factually you got your second table based on a fake approximation of third order therefore.

[marianoju]

Thanks for the hint, I did not know I could attach (.ods) files to my post! I find that my charts get dislocated everytime I close and open my .ods file (I have tried to Anchor To Page and Anchor To Cell) and I thought the screenshots to be most easily readable. I have now attached my files to my post.

[Lupp]

From my comment on the question:
“Did you already try a polynomial approximation using LINEST()? (Do you know how?)
355^4 is about 1.6*10^10. The predefined format of the topmost coefficient surely suppresses significant digits. Factually you got your second table based on a fake approximation of third order therefore.”

Using approximative / numeric tools always consider the expectability of such issues.

See this demo.

BTW: For the given data I would never use P4 but P3 (or P5). Was there a theoretical reason to use P4?

[marianoju]

@Lupp Thanks! I appreciate your help in a polynomial approximation using LINEST() which I knew of but had not tried to apply. Nevertheless my post was mostly motivated by my need to understand why my approach does not work. I understand that your (implicit) answer to my third question (“How do I calculate y given x using the ‘Trend Line Equation’?”) is better not approximate the polynomial curve this way. The trend line equation only displays rounded values (accuracy depending on predefined format) and the negligence of significant digits leads to an increasing error.

I used a polynomial regression with 4 degrees for convenience – it seemed like a reasonable compromise with a good coefficient of determination and a concise equation. Why would you suggest using three or five degrees?

Would you care to provide a comment on my first and second question?

[Lupp]

@Quoting @marianoju: “Would you care to provide a comment on my first and second question?”

1. Surely, but I don’t feel really competent insofar, and I even distrust so called "good practise to some degree.
2. There is a huge mathematical approximation theory. You may find expertise meeting your needs in the web if you define your needings.
3. I would assume the polynomial trendline and the LINEST results are based on the same algorithm. You only don’t get out the trendline coefficients with the needed precision. The equation is formatted badly. As most of numerical results in science and enginering fprmatting to a reasonable number of significant digits should be done instead of to a fix number of decimals. Such nonsense may be caused by bad standards induced by MS.
   Degree: The raw diagram is telling my eye that it’s roughly centrosymmetric. An approximating function suspected to be polynomial in addition we should expect the leading power to be odd.