I WANT TO GENERATE RANDOMNLY 9 NUMBERS IN EXCELSHEET CELLS 3X3 OUT OF 36 NUMBERS
Please don’t use capitals, it’s like shouting in the web.
And I think there are some threads about this. Like How to generate random non-repeating cells from a starting range?
without and duplicate are not tags, but essential parts of the question.
You can simulate the process of such a “multiple draw” by removing the drawn elements in succession, as demonstrated in the excellent example by @mikekaganski. This ensures a random “even distribution” probability, but makes for a fairly complex formula structure. Easily done in a procedural language, but in the functional language of spreadsheets it gets fairly bulky and/or convoluted. Kudos to MK for laying this out in a coherent and comprehensible manner. It is not easily accomplished.
A different approach which, as far as I can tell, yields the same end result with a fairly simple structure, and which is easily extendable:
-
Generate a list of 36
RAND()numbers.
Due to the nature of the pseudorandom numbers generated, there will not be identical numbers in the list (like there might be, though highly unlikely, with truly random numbers). -
Extract the
RANK()of the first 9 (or any 9) numbers in the list, and use those ranks as your drawn numbers
When the distribution of pseudorandom numbers is even, the probability distribution of those ranks should also be even. As long as the numbers are all different, the ranks within the range will list every number from 1 to 36 exactly once, in random order.
See attached file, where the extensibility is also shown.
You need first 9 elements of a sequence generated by sequentially picking and removing a random number out of 1…36.
Put this to A1 (use Ctrl+Shift+Enter to finish entering the formula, to create an array formula):
=LARGE(ROW(A$1:A$36);RANDBETWEEN(1;36))
Put this to A2 (use Ctrl+Shift+Enter to finish entering the formula, to create an array formula):
=LARGE(ROW(A$1:A$36)*(COUNTIF(A$1:A1;ROW(A$1:A$36))=0);RANDBETWEEN(1;36-COUNT(A$1:A1)))
Then select A2, copy to clipboard, select A3:A9, and paste.
What does the formulas do? The first one simply picks a random number between 1 and 36. It could of course be simplified to just
=RANDBETWEEN(1;36)
but I made it to resemble the rest of formulas in the column, for uniformity (as possible).
The second and following formulas generate a sequence of numbers from 1 to 36 (using ROW(A$1:A$36)), and make those elements in this sequence that already appear above to be 0 (multiplying the number by boolean COUNTIF(A$1:A1;ROW(A$1:A$36))=0 in array mode). So let’s imagine A1 was 12. The sequence from ROW(A$1:A$36)*(COUNTIF(A$1:A1;ROW(A$1:A$36))=0) would be
1 2 3 4 5 6 7 8 9 10 11 0 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
(because for 12, COUNTIF(A$1:A1;12)=0 would return FALSE, i.e. 0). The sequence has exactly 35 distinct values greater than 0; and given that we are calculating 2nd value, and only 1 value is above, the upper argument to RANDBETWEEN would be 35. Now we get a number of random rank varying from 1 to 35 from this sequence using LARGE, never picking zero values.
Now you have these nine numbers. If you need to put them into a 3x3 frame, just put this to B1:
=A4
and drag-copy to B3; put this to C1:
=A7
and drag-copy to C3. Now you may hide rows 4-9.
This method might be extended when you have some specified values, not necessarily 1…36, and not even necessarily contiguous. In that case, the numbers returned by the formulas should be considered indices into the array of the explicitly given numbers.
A10:A36 must remain empty?
@LeroyG: Why? you may extend the formula down to row 36 (e.g., to check correctness  ). It’s just unnecessary for the task of generation of 9 numbers
). It’s just unnecessary for the task of generation of 9 numbers 
@mikekaganski, I just tried with your answer, and wrote some data in A10:A36 with no adverse results. I asked, because the formula references until A36.
Formula only references those cells in context of ROW function, which returns the row number of the referenced cell irrespective of the cell’s content.
This is one of the many possible options.
Since we need to distribute 36 values between 9 cells, it is enough to select for each cell its own range no longer than 36/9 = 4 and we have to take care not to duplicate values.

With this method, the value 36 will appear very, very rarely.
You can use another method. Now for the first cell there are almost no restrictions, it can take any value from 1 to 28. And for the rest of the cells there are fewer and fewer acceptable values.

With this method, you can get the sequence 28,29, … 35,36 much more often than 1,2,3,4,5,6
There are other ways to generate random values. The choice of the best one depends on the task that is presented to the random number generator.
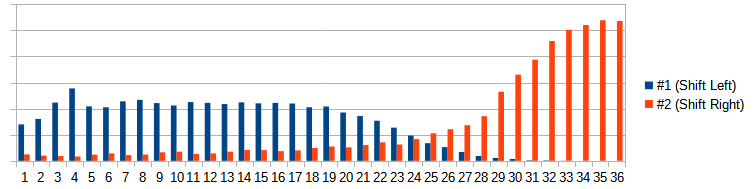
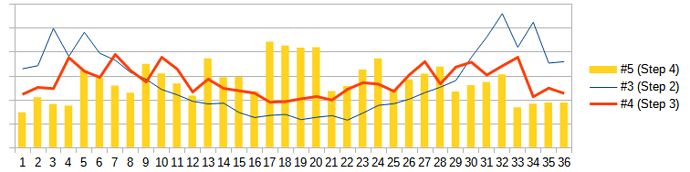
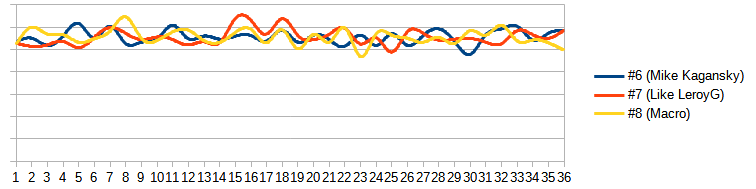
Update Since additional questions and solutions arose, I conducted a small analysis of the proposed algorithms.
The two solutions proposed above have the following distribution
If we start filling in 9 desired values from the middle of the list (from the fifth element) and change the step of changing the parameters, then we can achieve such results with the same RANDBETWEEN() function
The last diagram compares the @mikekaganski, @LeroyG and macro variants - all three are nearly identical.
Code:
Function getShuffled(iStart As Integer, iFinish As Integer, _
hSize As Integer, vSize As Integer) As Variant
Dim aTemp As Variant, aRez As Variant
Dim i As Integer, j As Integer, k As Integer
Dim iSh As Integer, jSh As Integer, kSh As Integer
Randomize()
Rem Create index array
ReDim aTemp(iStart To iFinish)
For i = iStart To iFinish
aTemp(i) = i
Next i
Rem Shuffle it
For iSh = iStart To iFinish
jSh = Rnd() * (iFinish - iStart) + iStart
kSh = aTemp(iSh)
aTemp(iSh) = aTemp(jSh)
aTemp(jSh) = kSh
Next iSh
Rem And shuffle again, backward
For iSh = iFinish To iStart Step -1
jSh = Rnd() * (iFinish - iStart) + iStart
kSh = aTemp(iSh)
aTemp(iSh) = aTemp(jSh)
aTemp(jSh) = kSh
Next iSh
Rem Array for result
ReDim aRez(1 To vSize, 1 To hSize)
k = iStart
For j = 1 To vSize
For i = 1 To hSize
If k > iFinish Then
Rem For the resulting array, more numbers were needed than
Rem are in the original set - reshuffle additionally
For iSh = iStart To iFinish
jSh = Rnd() * (iFinish - iStart) + iStart
kSh = aTemp(iSh)
aTemp(iSh) = aTemp(jSh)
aTemp(jSh) = kSh
Next iSh
For iSh = iFinish To iStart Step -1
jSh = Rnd() * (iFinish - iStart) + iStart
kSh = aTemp(iSh)
aTemp(iSh) = aTemp(jSh)
aTemp(jSh) = kSh
Next iSh
k = iStart
EndIf
aRez(j, i) = aTemp(k)
k = k + 1
Next i
Next j
getShuffled = aRez
End Function
Call it like as
{=GETSHUFFLED(1;36;3;3)}hello @JohnSUN: imho none of your receipts produces random numbers (despite using rand functionality), you mentioned yourself that 36 (and other high numbers) will be under-represented in 1. ver., in second ver. there will be too few small numbers as each subsequent number is limited to the range above the max of the former numbers,
and … your numbers will be sorted, what is normally not the case for random numbers …
The thing is, @JPMAKWANA spent too few words on the task description. Therefore, it seems to me that it makes no sense to require a random order of numbers in the resulting table. As I mentioned in my answer, there are many different solutions for similar tasks. We can achieve very different distributions of numbers in the matrix simply by changing the parameters of the RANDBETWEEN() function. We can get almost any result with a macro. But we will not be able to accurately answer the incompletely asked question.
(I don’t mind your statement “none of your receipts produces random numbers” because I don’t understand what you are writing about.)
@JohnSUN: the values generated according to your recipe are not ‘randomly evenly’ distributed over the number range from 1 to 36, but accumulate in the lower part of this range in one version and in the upper part in the other version, this doesn’t have to be immediately noticeable, but if you repeat the attempt more often you will notice it, and someone who - e.g. in a lottery - prefers to bet on the ‘more frequentet numbers’ would have better chances of winning, thats what i meant with ‘not random’ …
Oh, you didn’t mean not “not random” but “not normally distributed”? Didn’t I mention this feature of the proposed options? Can you argue that the author of the question is not looking for just such a solution - shifted to one of the edges? Are you sure this is a lottery game, not a fireworks design?
@JohnSUN: no, sorry, careful, ‘normally distributed’ is a special spreading around a median with a ‘belly’ curve to both sides - afaik, that’s also ‘not random’,
really ‘random numbers’ as for a lottery should be … random … not all the same, distributed in the desired range, and - for large quantities - so evenly distributed that a prediction is not possible, also no prediction like ‘probably higher numbers are more likely to occur’, this is not fulfilled by your methods,
a random number between 1 and 36 should have the same 1/36 chance for every draw, your samples have smaller restrictions which numbers are possible or ‘likely’ for each cell,
the special lottery case - where a drawn number is not given back to the pool - (no duplicates) looks like having only 1/35 of each leftover chance for the second draw, but as you have to consider 36 different cases for the 36 possible results of the first draw it calculates back to 1/36 chance for each value,
@JohnSUN: very nice work!, 

 , yes, that’s it, a ‘random functionality’ should hold in a test of the distribution of the results … have seen a test shortly that nearly no! OS passes this test with it’s rand funcion if you go deeper and evaluate predictability, linux was among the best!
, yes, that’s it, a ‘random functionality’ should hold in a test of the distribution of the results … have seen a test shortly that nearly no! OS passes this test with it’s rand funcion if you go deeper and evaluate predictability, linux was among the best!
would like upvoting to honour your efforts, but the other answers are easier for new questioners searching a solution,
you need not shout / cry (capitals) for that, save it for important news like EX$EL SPREADS CORONA or similar,
steps:
- produce some random values with “=INT(RAND()*36+1)”,
- copy and paste their values (not formula) with strg-c shift-strg-v,
- apply advanced filter to that range, the range itself as filter criteria, options ‘no duplicates’, ‘copy output to’,
- for a 3x3 array copy first 9 cells from that output with “=”,
- looks you are done,
- left: check mathematical correctness,
- left: automate steps,
- left: transfer to ex$el,
- left: care to produce enough input in step 1.,
- limitation: as there is no limit how many identical valus the rand() function may produce in a row the procedure may fail with any amount of input,
alternatively: watch the lottery of your choice with at least 9 pulls from at least 36 chances and note the first 9 fallen numbers below 37 into a sheet, if you are unlucky and get too few numbers (too many values above 36) continue next week and manually eliminate duplicates,
My answer based on how I understand the question.
Given 36 whatever numbers in a list, select randomly 9 numbers, and show them in a 3×3 cells range.
- A2:A37 contains an ordered list from 1 to 36.
- B2:B37 contains all 36 numbers to choose from.
- D2:F4 is the 3×3 cells range in which to show the 9 numbers chosen:
=VLOOKUP(INT(RAND()*36+1);$A$2:$B$37;2;0). - use
=MODE(D2:F4)to visually evaluate if there are repetitions, pressF9until formula show #VALUE!. - copy D2:F4 and paste as unformatted text (choose menu
Edit-Paste Special-Paste Unformatted TextorCtrl+Shift+Alt+V) in a separate range to not lose the formula.
More LibreOffice Help on RAND, INT, VLOOKUP, and MODE.
If you are working with LibreOffice since version 7, instead of RAND, use RAND.NV. You will need to select D2:F4 to recalculate the values (with F9), but will no more need to do the last step; NV stand for non-volatile.
Press edit below your question if you want to add more information; also can comment an answer (Add Answer is reserved for solutions).
Check the mark (![]() ) to the left of the answer that solves your question.
) to the left of the answer that solves your question.