calc: are decimal correct calculations possible?

[newbie-02]

hi @all,

!!! Caution! this is ‘in progress’, and I just noticed errors where I have to sort what are thinking errors of me and what are inadequacies of calc or tools (rawsubtract), see comments, I will adjust the question and example sheets based on my progress, sorry, maybe I started the discussion too early, but I need it - the discussion, and the results so far look so good that they certainly still have errors, this is normal, but probably will not fail completely … !!!

there are a few - imho too many - questions on the internet ‘why doesn’t my spreadsheet calculate correctly?’

a few of the ‘classics’ are:
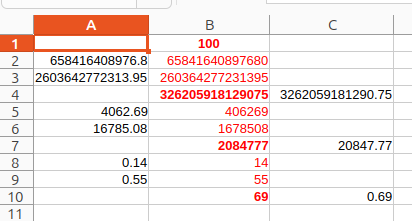
'=0,1 + 0,2 ’ results in 0,300000000000004 instead of 0,3,
‘=1234,12 - 1234’ results in 0,119999999989100000 instead of 0,12 and
‘=0.043 - 0.042’ results in 0.000999999999999400 instead of 0.001,

attached is a sheet which calculates (more) correctly with a few primitive tricks, I would be glad if people with knowledge of the matter would have a look at it,

sample sheet, click for download

[edit - adding another version of the sheet, added a macro formula for calculation, and saved in tdf 1.2 extended format]

sample sheet with macro and in 1.2 format, click to download

i hope i included all neccessary macro help functions …

[/edit]

mostly such questions are answered with ‘that’s how floating point maths is, but it’s fast’, ‘learn first what that is (floating point mathematics)’, ‘it must be like that’, ‘we can’t change it’, ‘look at Weitz (www.weitz. de/ieee), “the error is correct”’, ‘ex$el calculates the same way’ and so on, the claim that a spreadsheet should and could calculate as ‘correctly’ as we once learned it in school is simply negated, either with ‘impossible’, or with ‘performance’,

I find this after 35 years of standard (IEEE 754) and 35 years of development (of LO calc) ‘a bit weak’, so it gets on my nerves so much that even comments like ‘spam’, ‘ignorant person’, ‘your pet peeves’ etc. didn’t deter me to think about it,

I think at least many of the problems ‘work better’, and users should be allowed to get real results even if they are different from ex$el,

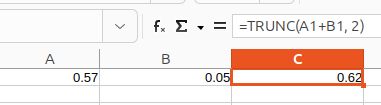
attached a sheet what shows that, red marked: wrong, green marked: better,

I don’t say that this is one or ‘the!’ final solution or ‘the last word’, but it is a clear proof that:

• for many cases better results are possible,
• they can be achieved with relatively little effort,
• for the users much more comfortable and
• are much less error-prone than if the users always have to stumble over errors first and then have to manage the rounding themselves after recommendations for workarounds,

I would like to have an open discussion about whether it would be better to implement such calculation - at least as an option - in calc, and if not then why not,

in this discussion could be discussed / clarified among other things:

• that there are completely different problems if decimals do not (can not) exactly match the IEEE binaries in which they are mapped, in contrast to the fact that certain calculations are difficult (cancellation in subtraction and absorption in addition), this is often ‘lumped together’ even by ‘professionals’, which hinders suitable problem solutions, the first is relatively painless, it’s just the way it is, and does no harm as long as the ways to (to binaries) and back (to decimals) match, ‘cancellation’ on the other hand can inject significant! errors, but you can ‘calculate out’ most of them !!!if you do it right away (on the intermediate result)!!!,

• that these errors may be marginal, but make significant differences e.g. for comparison operations (=?, >?, <?) and cause wrong results for MOD, number series, downfills etc.,

• whether it is right to fight the errors with ‘arbitrary untargeted rounding’ which in my opinion causes errors in other places, and rather bigger ones,

so … I am happy to receive opinions, and also criticism …

reg.

b.

[ml9104]

The problem is, that you expect insane decimal precision from an IEEE-754 40-bit or 80-bit FPU. Even though 80-bit floating-point has a high degree of precision, it still is limited to, you guessed it, 80 bits.
No one would use that many digits in practice, we’re talking about decimal fractions that are completely impossible in the real world.
This is why exponential notation was invented.
It reminds me a bit of very green engineering students measuring a 5% resistor and then calculating the value to the 20th decimal.

Funny that you send us an Excel spreadsheet on a Libre Office site, though.

[newbie-02]

hello @ml9104,
that you expect insane decimal precision … no!, what i’m fighting is use of such hardware in a way producing ‘visible’ fails,
64-bit doubles have space for 1 micrometer accuracy for the distance earth - moon, calc fails on 0,043 - 0,042,
we're talking about decimal fractions that are completely impossible in the real world … no!, i’m talking about calculating money to cents, distances to millimeters, times to seconds, correct!,
measuring a 5% resistor and then calculating the value to the 20th decimal. … bridge construction: calculate to the seventh decimal and then take it ‘times two’, that schould hold,
Funny that you send us an Excel spreadsheet on a Libre Office site, though. … häh? it’s an *.ods made with LO calc 7.2.0.0.a0+, perhaps it’s saved as ‘tdf1.3’, would you like it in 1.2?

[Regina]

@newbie-02

i’m talking about calculating money to cents, distances to millimeters, times to seconds, correct!,

Then calculate in the smallest needed unit and write own routines for rounding, that reflect the legal rules in that area. Separate calculations from presenting the results.

[newbie-02]

@Regina

Then calculate in the smallest needed unit and write own routines for rounding, that reflect the legal rules in that area. Divide calculations from presenting the results.

hello Regina, nice to read from you, that is one of the more powerful proposals which mostly work, same hint from a reputed math professor: “For simple calculations, just multiply all numbers by 100 so that you get exact integer amounts in cents rather than inexact fractional numbers in $ or € or whatever the currency is called.”, and some counterexamples:
( 658416408976.8 * 100 + 2603642772313.95 * 100 ) / 100 → 3262059181290.7505 ,
( 4062.69 * 100 + 16785.08 * 100 ) / 100 → 20847.770000000004 ,
( 0.14 * 100 + 0.55 * 100 ) / 100 → 0.6900000000000002 .
So not yet the final solution.
And… what entitles us to let every user naively believe that Calc calculates correctly, then let them fall into traps - which they may not notice - and then expect them, as laypeople, to deal with the construction of workarounds… every single one of them… that’s perverse, user trapping, and a waste of working time.

[CRDF]

@newbie-02

and some counterexamples:

?

[newbie-02]

@CRDF

?

“then let them fall into traps - which they may not notice”,
“And always be aware that Calc doesn’t show you the exact value calculated to or used to calculate ( in background ), however something castrated to 15 digits” … thus often the result looks right while isn’t. It covers up for some time and then punches through and ( nearly ) nobody can explain.

[CRDF]

But it is my understanding that e.g. accounting/currencies have TRUNC(_, n)
(?)

[newbie-02]

with trunc undershot results would fail in bin-FP math, e.g. 0.57 + 0.05 → 0.61, round would help better, however bin-FP rounding to 2 decimals places is carried out by * 100, + 0.49999999999999994, trunc, / 100 and will also fail, just for other cases.

[CRDF]

@newbie-02

e.g. 0.57 + 0.05 → 0.61

?

By the way: “decimal calculations” by pencil & eraser were made by truncation.
I’ve seen small inventories for the yearly balance being computed via desk calculators, pencil & eraser (literally).
[Quantity x “cost $”] →discard figures after ,nm (the cents). Cross them out.
Idem for, by hand, say ⅓
x |____ ←(3 here)
… do it up to ,__ and stop.

[newbie-02]

@newbie-02

e.g. 0.57 + 0.05 → 0.61

Sorry, copied from wrong row or typo, try 0.54 + 0.57, Calc will display 1.11 and trunc to 1.11, however that’s combining faked display for IEEE result 1.1099999999999999, and “fuzzy rounding” with a 4 bit? “snap to zero”. Here working correct, but try to estimate how long it will hold. Or memorize the already mentioned “There is nothing exact in floating-point calculations in Calc, …”, Mike Kaganski 2023 in “comment #5 in Calc Round Down is Rounding Up for some values”, * [Online]. Available: 154792 – Calc Round Down is Rounding Up for some values, retr: 2025-05-13, mentioned in C#54 here, and evaluate the title of that thread reg. reliability of trunc ( which is rounddown direction 0 ).

[CRDF]

My approach here tries to be the practical use of Spreadsheets (here = Calc of course), not a theoretical one.
So users must be aware of floating point arithmetics. For e.g. Accounting, employ TRUNC according to local currency.
For other professional fields, also the user (we Engs. etc…) must employ the tool (Spreadsheet) accordingly.

Yes: perhaps SO sophisticated softwares in XXI Century could have a “type” like a true “decimal(_, n)” – no roundings at all. But I’m not able to argue about that (?)

[newbie-02]

@CRDF

sophisticated softwares in XXI Century could have a “type” like a true “decimal(_, n)”

second that.

[Villeroy]

LibreOffice comes with a database component supporting dozens of database engines where this is a matter of course.

[mikekaganski]

In your sample document, you are rounding the result of subtraction to the position of 15th decimal digit of the greater of the original values. So your idea is to limit the precision of calculation to “fix” catastrophic cancellation.

Your idea is not new; also it is not correct. Your idea is about assumption that what is displayed in cell is closer to “ideal” value than what is actually there. It might be true only with very limited set of cases, where the values in cells are manually typed there by user, and only addition/subtracted is used.

But it would make most real calculations worse. Consider any trigonometric functions where you use radians, or any logarithmic functions, or even simple multiplication/division. There you get more “significant” digits than were in initial numbers that user had entered. And arbitrarily limiting the precision of those numbers would result in much worse catastrophes universally.

For instance, take this simple calculation of well-known triangle and its scaled variant:

        A                  B
1       3               =A1*PI()
2       4               =A2*PI()
3       5               =A3*PI()
4 =SQRT(A3^2-A2^2) =SQRT(B3^2-B2^2)

In ideal world, A4 must be equal to A1, and B4 to B1. In Calc, although the value of PI() is naturally imperfect, RAWSUBTRACT(B1;B4) also shows 0. But if in B4 we replace SQRT(B3^2-B2^2) with your SQRT(ROUND(RAWSUBTRACT(B3^2;B2^2);15-MAX(ROUND(LOG(ABS(B3^2);10);0);ROUND(LOG(ABS(B2^2);10);0)))), we suddenly get the difference between B1 and B4 by 1.77635683940025E-15.

Carefully prepared limited-precision input in your sample is not representative. Note that I don’t talk about performance here, I only talk about precision that you try to achieve. Your approach would fail miserably in all but simplest cases. Current implementation of subtract is of course not ideal (in this non-ideal world), but you may notice that it still tries to be reasonably smart using rtl::math::approxSub which handles near-zero result (unlike the implementation of RAWSUBTRACT, which tries to be simple).

[newbie-02]

hello @mikekaganski,
thanks for your help,
rounding acc. the greater operand may be wrong, acc. the smaller may be better, it’s experimental,
i just stumbled over 29,999999999999900000 if i wrap rawsubtract in a macro:

function rawsubtract_a (ByVal darg1 as Double, darg2 as Double)
oFunctionAccess = createUnoService( "com.sun.star.sheet.FunctionAccess")
rawsubtract_a = oFunctionAccess.callFunction( "RAWSUBTRACT", array(darg1, darg2)) 
end function

and call ‘=RAWSUBTRACT_A(33,0000000000001;3,0000000000001)’,

i used it in an attempt to stay away from 4-bit truncations and similar, will try to improve,
it’s a general problem being limited to use imperfect tools to improve just these tools …
‘trigonometric functions’: yes, but:

1. the average user wants correct subtractions first,
2. the fail may result from other shortcomings than my idea? see above,
3. I don’t refuse to improve my idea, I just refuse to carry on too glaring errors in calc,

[newbie-02]

my samples are targetting ‘massive cancellation’ when subtracting similar values,
@mikekaganski’s sample deals with values with significant difference,
adapting the formula to apply less tight rounding to ‘more different’ values should be simple …
as - perhaps that’s a good idea - don’t touch integers?
in the end it may require a ‘case differentiation’ between ‘one operand zero’, ‘addition’, ‘subtraction of identic’, ‘subtraction with very small difference’, ‘subtraction with small difference’, ‘subtraction’,
why not, progress justifies some effort …
the performance part will come later, it is! important, i think i can! solve,

[mikekaganski]

‘trigonometric functions’: yes, but:

1. the average user wants correct subtractions first,

No. Please write “I want that first”. It’s the usual thing, that you claim something to be general rule when you have no idea about demographics of usage of the product. There’s no “But” here, it must be correct everywhere.

2. the fail may result from other shortcomings than my idea? see above,

Absolutely unclear what you mean.

3. I don’t refuse to improve my idea, I just refuse to carry on too glaring errors in calc,

There’s nothing to discuss until there’s an idea. There is clear understanding that what you ask is generally impossible, among those who have substantial knowledge in the topic. You insist on “it must be possible, I don’t believe you, I’m not listening lalala”. Ok, that’s fine, but that’s your task to come with the viable idea. You came with something that is absolutely old and wrong; I took time to explain why. Up to you to come with something else.

[mikekaganski]

There’s a general rule: extraordinary claims require extraordinary evidence. Your claim (“there is some method to make it perfect or at least generally better using IEEE numbers”) is extraordinary one. It doesn’t mean it’s necessarily wrong, (although I’m sure it is) but it needs extraordinary proof. E.g., a great analysis which would prove it’s (more) correct in general case, or that tests the whole range to confirm that claim. Yes, testing square of 4 billion possible numbers (to at least prove it for 32-bit float case) is impossible. But then at least use some possible number of uniformly spread numbers, and make an analysis on those.

[newbie-02]

@mikekaganski:

• you’re right, rounding results makes sense with ‘round’ operands, and may harm ‘special values’ (besides that the accuracy you use is outside the ‘15 digit range’),

• importance of targets … imho 95% of calculations with calc are accounting and similar, less than 5% of users will use pi() or similar anywhere,

• my wish: fulfill both! targets,

• in an attempt to decide where to round and where not and to use ‘-’ as you said better than rawsubtract i stumbled over an old problem:
  @ajlittoz: i doubt in calcs “correct math” (over the subset of Q …), try following calculation:

  A1: =22
  B1: =63,999999999999+A1*10^-14
  C1: =-63,999999999999
  D1: =A2+A3
  E1: =RAWSUBTRACT(A2;-A3)

vary A1 between 30 and -30 and observe results in D1 … other people had a similar wish - correct math - and to achieve that for some special cases (result ‘0’) they äh … (brutally raped?) … calcs precision … is there any option to switch that off?