Average the last value from up to 8 possible subsets

[LeroyG]

Hello all,
I need to average the last value from up to 8 possible subsets each having up to three values (first and/or second value may be missing).
I need to apply this formula to less than 100 rows.

After a few failed solitaire attempts with IF, IFS, CHOOSE and more (see below the shared file), I searched in the site, and found a formula (thanks to @JohnSUN for sharing it) that I was able to transform from column to row.

How do I sum the last 12 values in a column?

Take your time to study this horror. Surely there are more elegant solutions. It’s just the first thing that came to mind. In this formula, OFFSET() repels from the very last cell in column B, backs up by 12 cells and shifts down again. If you start from B1, then you can do without INDIRECT() =SUM(OFFSET(B1;SUMPRODUCT(MAX(IF(B2:B10000="";"";ROW(B2:B10000))))-12;0;12;1)) Most likely this can be improved.

This is the formula for the first subset (remember that I need to average 8 subsets).
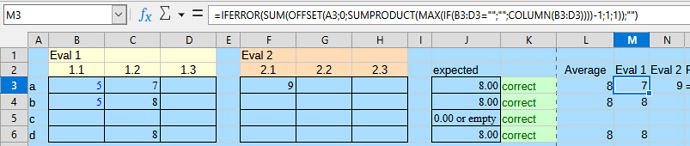
=IFERROR(SUM(OFFSET(A3;0;SUMPRODUCT(MAX(IF(B3:D3="";"";COLUMN(B3:D3))))-1;1;1));"")
Although I don’t understand it thoroughly (I hope some day to know a bit more), it works.

So, my question:

Could it be a shorter or simpler formula to solve this?
Thanks in advance.

Sample file: average of last values if there.ods (35.3 KB)
Here is a screenshot with the working formula tested on 4 rows (the first with 2 subsets).

[joshua4]

Can I use this question to ask a more general one? Is there a way to handle an array the way you handle a range with OFFSET?

Here, for example, I can neatly collect the values using implicit modular math with SEQUENCE and OFFSET, and I can then find the answer again using OFFSET…but I have to have the explicit array in a range to do that.

So, starting with something like =OFFSET($A$18,0,SEQUENCE(1,3,0)+SEQUENCE(8,1,1,4)) then nesting that into something like =SUMPRODUCT(MAX(OFFSET(C4,SEQUENCE(8,1,0,1),0,1,3))) /3, where instead of the OFFSET(C4…) we cleverly use INDEX or something on the first function, which would be like doing it on C4:E11, I suspect.

In essence, is there a way to nest the yellow function into the orange one on the enclosed spreadsheet? It seems like, if there is, that would be a great generalization for problems like these.

Averages and Array Instead of Range.ods (35.0 KB)

[koyotak]

I can’t develop any logical argument from your screenshot and your file, let alone derive any mathematical average. Your task isn’t congruent!

• a)

Summary

values can be integers between 1 and 10: so 2, 3, 4, …, 7, 8, 9. Or inclusive 1 and 10?

Summary have i deleted! <

• b) the average have to be from the last value of each eval done, the handycaps are all the “empty” cells.
• b.1) what do you mean by “the last”? Is it the highest integer of the row pro Eval? Or is it the most right aligned integer without empty cells so it can be lower than any value in left cells?
• b.2) do the integers have to increase from left to right within the 6 cells from “1.1” to “2.3”?
• where are the 8 possible Evals? I can only see two: “Eval 1” and “Eval 2”.
• what do you mean by “each with 3 possible instances”? I suspect: in each row [Bn:Hn], “1.1” to “2.3”, there can be an integer in 0…3 cells.

[Lupp]

For your example data the last entry in every eval triple is also the largest one in the strip.
If you (@LeroyG) can assure that this will also be the case with your real data, the solution is simply to use MAX().
If not (what I would expext), the example is very misleading.
I made an example with random numbers and 4 groups of different width.
It uses the functions LET() and SEQUENCE(), and will therefore only work with LibO V24.8 or higher.
average_of_last_values_per_group.ods (25.5 KB)

[koyotak]

@Lupp

For your example data the last entry in every eval triple is also the largest one in the strip.

I had suspected that

[sokol92]

Try

=IFERROR(AGGREGATE(1;6;LOOKUP(1E+099; B3:D3);LOOKUP(1E+099; F3:H3));0)

There can be any number of ranges, and the number of columns in the range can also be any.

[LeroyG]

@koyotak

Your task isn’t congruent

Maybe. Thanks anyway to engage on it.

a) values include 1 and 10.
b.1) the last is the rightmost occupied cell of each Eval.
b.2) new values may be lower than previous ones (but this is not the expected)

@koyotak

where are the 8 possible Evals?

A button (or two) is enough. And the near 100 rows? With 4 is enough.

@koyotak

what do you mean by “each with 3 possible instances”?

n.1, n.2, n.3, where n can be 1 to 8 (only 1 and 2 in the sample file).

@Lupp

For your example data the last entry in every eval triple is also the largest

So, my sample is faulty.

@Lupp

It uses the functions LET()

The spreadsheet will be used by another people, and I don’t know which LO version they have. Anyway, I can beware them to update.
Your formulas reminds me the little that I know.
Thanks.

Tomorrow, at work, I will test with the real data. Many thanks to all of you.

[koyotak]

000_LO-CALC_log and avg of 2 blocks_v0003_075005.ods (35.1 KB)

In the morning at work I had to relieve my sleepy brain of its simple solution.

[koyotak]

thats my combinated solution logically and mathematically

• a) with aux columnes
• b) with complexe MAX()-functions
• c) with new LET()-function,

by searching for the highest so more right aligned integer pro “Eval”-row
000_LO-CALC_avg of max values of 2 blocks_015357.ods (36.9 KB)

---

If you think a lot about the different options, you will come to a very simple solution if only the rightmost cell value is needed:

=iFS(SUM(B3:D3)=0, 0, D3>0, D3, C3>0, C3, B3>0, B3)

• case 1: the 1st argument if the 3 cells are empty, if not:
• case 2: if the most right aligned cell [D3] is not empty, than output D3, else:
• case 3: if the middle aligned cell [C3] is not empty, than output C3, else:
• output B3!

What a crasy Simplicissimus! What an insult to my powerful macMini M4 chip because there is nothing to do but first class logic.

[Lupp]

The IFS() formula is simple and efficient. :applause: (Emoticon missing?)
I wouldn’t have found it because of a tendency to generalise problems in the first step.

[koyotak]

@Lupp

I wouldn’t have found it

My monkey in my brain reminded me of my computer science studies.

[fpy]

@Lupp

missing …

[koyotak]

@Lupp

The IFS() formula is simple and efficient.

only for studying the basic-to-the-roots programming for those who can think binary and comparatively:
1_LO-CALC_LET()-iFS()-comparators_study-v000_021316.ods (51.8 KB)

---

In conclusion: It’s shameful that it took me so long to get back to basics programmatically, because every computer language is astonishingly stupid and will remain so! Thus, only bit values are compared with each other in AND, OR, and NOT gates. The “new” LET() function is nothing more than an ancient PLC block in which subfunctions can be elegantly integrated hierarchically – in my study and this one, using binary elements and without any calculations having to be duplicated.

Logic thought differently: In contrast to hardware electronics with semiconductor gates (ICs), software only allows for a relatively slow, line-by-line processing of instructions like human reading any book, which only creates problems or can be elegantly exploited, as used here, by checking successively whether an expression/comparison is valid and then aborting this procedure until an expression is valid.

This morning, I recognized the genius of the LET() function and studied it in detail to avoid complex functions like LOCKUP() with its dubious OUTPUT in the future, as well as the difficult-to-modify matrix{} arrays that I had spent hours agonizing over. Even if I archive this file solely for my own study, I hope at least one reader will learn something from it. In any case, not everyone is taught digital logic.

---

PS in DEU: Mit den komplexen undurchschaubaren Matrix{}-Funktionen stehe ich weiterhin auf „Kriegs-Fuß", wegen deren nicht vorhersehbaren und nicht erwünschten Ergebnisse! Obwohl ich sie mag, eben wegen ihrer Komplexitäten, speziell SVERWEiS/WVERWEiS/VERWEiS (LOCKUP).
Warum einfach, wenn es auch irgendwie kompliziert geht?

[LeroyG]

@koyotak

=iFS(SUM(B3:D3)

I worked with auxiliary columns (in a hidden sheet), because I found no way to include empty arguments in the average function.
Thanks all who contributed to decrease my ignorance.

[sokol92]

@LeroyG

Thanks all who contributed to decrease my ignorance

What are the shortcomings of my formula?
The result matched on all rows.

[Lupp]

The question wasn’t addressed to me. However, I willl answer.

@sokol92

What are the shortcomings of my formula?

None so far except…
that I could never have found it in years.

I used LOOKUP() very rarely, and I never use AGGREGATE() or any function with parameters which are “cryptic” to me due to my very limited memory.
Now I took the chance to try it, and I got the columns AH through AJ of the attached example which may convince other visitors of the efficiency and reliability of the solution by @sokol92. (Forget AA through AG.)
disask124184_average_of_last_values_per_group.ods (26.7 KB)

[sokol92]

@Lupp

I never use AGGREGATE() or any function with parameters which are “cryptic”

AGGREGATE was specifically designed to be able to ignore error values, subtotals, and hidden rows during group operations. Nobody (except formula fans) remembers the parameters of this function, you can always look it up.

[sokol92]

@Lupp

I used LOOKUP() very rarely

The LOOKUP function is implemented in such a way (Calc, Excel) that the construct

=LOOKUP(VeryLargeValue; Range)

returns the value of the last non-empty cell in a Range consisting of one row and several columns (or several rows and one column).
This is not explicitly stated in the documentation, but has been frequently used in Excel for the last 25 (at least) years.


Update.
More clever tricks are possible.
The following formula will find the last non-empty, non-zero cell in range B2:M2.

=LOOKUP(1E+100;1/(B2:M2<>0);B2:M2)

[LeroyG]

@sokol92

the shortcomings of my formula

None for me directly; but as I didn’t have time to test in other environments, and I can’t control if the spreadsheet will be used with LibreOffice (and with which version) or with another program, I stuck with what seemed safe to me.
Could you (@sokol92) put it as an answer, so we can upvote it?

[sokol92]

@LeroyG

Could you (@sokol92) put it as an answer, so we can upvote it?

@LeroyG , thank you for the interesting topic, I think readers will learn a lot of useful things from it.